Rolle's and Mean Value Theorems
The Mean Value Theorem (MVT, for short) is one of the most frequent subjects in mathematics education literature. It is one of important tools in the mathematician's arsenal, used to prove a host of other theorems in Differential and Integral Calculus. As a curiosity, it is most frequently derived as a consequence of its own special case -- Rolle's theorem. The latter is named after Michel Rolle (1652-1719), a French mathematician who established the now common symbol  for the nth root and insisted that -a > -b, for positive a and b, a < b. The feat went against Decartes' teaching and laid the groundwork for the introduction of the ubiquitous number line.
Rolle's Theorem
Let f be continuous on a closed interval [a, b] and differentiable on the open interval (a, b). If f(a) = f(b), then there is at least one point c in (a, b) where f '(c) = 0.
(The tangent to a graph of f where the derivative vanishes is parallel to x-axis, and so is the line joining the two "end" points (a, f(a)) and (b, f(b)) on the graph. The line that joins to points on a curve -- a function graph in our context -- is often referred to as a secant. Thus Rolle's theorem claims the exsitentce of a point at which the tangent to the graph is parallel to the secant, provided the latter is horizontal.)
Mean Value Theorem
Let f be continuous on a closed interval [a, b] and differentiable on the open interval (a, b). Then there is at least one point c in (a, b) where
| (1) |
f '(c) = (f(b) - f(a)) / (b - a).
|
(The Mean Value Theorem claims the existence of a point at which the tangent is parallel to the secant joining (a, f(a)) and (b, f(b)). Rolle's theorem is clearly a particular case of the MVT in which f satisfies an additional condition, f(a) = f(b).)
The applet below illustrates the two theorems. It displays the graph of a function, two points on the graph that define a secant and a third point in-between to which a tangent to the graph is attached. The graph and the three points on it are draggable.
Proof of the Mean Value Theorem
Assume Rolle's theorem. The equation of the secant -- a straight line -- through points (a, f(a)) and (b, f(b)) is given by
| |
g(x) = f(a) + [(f(b) - f(a)) / (b - a)](x - a).
|
The line is straight and, by inspection, g(a) = f(a) and g(b) = f(b). Because of this, the difference f - g satisfies the conditions of Rolle's theorem:
| |
(f - g)(a) = f(a) - g(a) = 0 = f(b) - g(b) = (f - g)(b).
|
We are therefore guaranteed the existence of a point c in (a, b) such that (f - g)'(c) = 0. But
| |
(f - g)'(x) = f '(x) - g'(x) = f '(x) - (f(b) - f(a)) / (b - a).
|
(f - g)'(c) = 0 is then the same as
| |
f '(c) = (f(b) - f(a)) / (b - a).
|
Remark
The above is rather a standard proof of a standard formulation. The motivation for the choice of the auxiliary function g(x) is often questioned and even considered obscure. (f - g)(x) represents the vertical distance -- difference -- between the two graphs: that of f and the secant which is the graph of g. Other functions g can serve the same purpose.
Let A, B, X denote the points (a, f(a)), (b, f(b)), and (x, f(x)), respectively. Then the distance d(x) from X to AB can be easily computed and then differentiated. A more elegant approach depends on the observation that the product of d(x) and the length |AB| of AB equals twice the area S(x) of  ABX. This area has a simple expression in determinants:
First of all observe that not unexpectedly S(a) = S(b) (= 0.) We are thus in a position to apply Rolle's theorem. The derivative S'(x) is given by
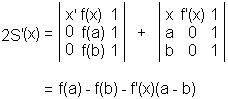
So that S'(c) = 0 immediately implies (1).
Both Rolle's and the Mean Value Theorem are statements of pure existence. Except for claiming that point c lies in the interval (a, b), neither provides more accurate information as to its location. For this reason, generations of students found the theorems perplexing. Following J. Dieudonné, R. P. Boas argued that the following form of the MVT is both more intuitive and no less useful:
Assume the derivative f ' of function f is bounded on (a, b):
Then
| |
(b - a)m ≤ f(b) - f(a) ≤ M(b - a).
|
For a function, which is the integral of its derivative, this is the same as
which, in turn, is a form of what is known as the Mean Value Theorem for Integrals:
If f is continuous on a closed interval [a, b], then there is at least one point c such that
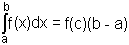
For further information and applications see superb pages by Timothy Gowers.
References
- A Century of Calculus II, T. Apostol et al (eds), MAA, 1992
- J. Dieudonné, Foundations of Modern Analysis, Academic Press, 1960
Copyright © 1996-2008 Alexander Bogomolny
|
