Two Circles and a Limit
Proof #2 by Stuart Anderson
We are solving the Two Circles and a Limit problem:
A stationary circle of radius 3 is centered at (3, 0). Another circle of variable radius r is centered at the origin and meets the positive y-axis in point A. Let B be the common point of the two circles in the upper half-plane. Let E be the intersection of AB extended with the x-axis. What happens to E as r grows smaller and smaller?
Let C be the center of the stationary circle. Draw the chord OB of the varying circle and consider the triangle OCB. This is of course isosceles, so the angle bisector at C cuts the chord OB at its midpoint D, and meets OB at a right angle. Therefore ∠AOB = ∠DCO = 1/2 ∠BCO. Next, look at triangle AOB, which is also isosceles, and repeat the same process, so that there is an angle bisector at O meeting chord AB perpendicularly at its midpoint F. Then since OF is perpendicular to BE, ∠BEO = ∠AOF = 1/2 ∠AOB.
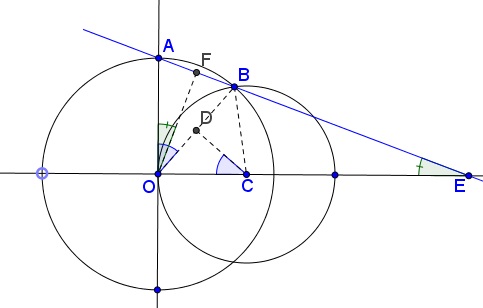
Therefore ∠BEO = 1/4 ∠BCO. This is true regardless of the size of r, so in the limit as r→0, B moves down to the origin and in the small angle limit we get OE = 4·OC. But OC = 3, so OE→12. One could put more details into taking this limit, but it is pretty clear that the ratio approaches 4. Although the algebraic methods also give the limit as 4, this appears somewhat mysterious. The fact that the angles BCO and BEO are in 4:1 ratio gives the clearest most satisfying way to see why the limit is 4, at least in my opinion.
Limits in Geometry
|Contact|
|Front page|
|Contents|
|Algebra|
|Store|
Copyright © 1996-2015 Alexander Bogomolny
