Two Circles and a Limit
Trigonometric Solution

We are solving the Two Circles and a Limit problem:

A stationary circle of radius $3$ is centered at $(3, 0).$ Another circle of variable radius $r$ is centered at the origin and meets the positive $y-axis$ in point $A.$ Let $B$ be the common point of the two circles in the upper half-plane. Let $E$ be the intersection of $AB,$ extended, with the $x-axis.$ What happens to $E$ as $r$ grows smaller and smaller?

The use of trigonometry was suggested by the NY math teacher Patrick Honner.

Let $\alpha = \angle AOB,$ with $O$ standing for the origin. Then $B = (r \sin \alpha,\; r \cos \alpha ),$ so that the slope of $AB$ is given by

$(r \cos \alpha - r) / (r \sin \alpha ) = - \sin (\alpha /2)/\cos (\alpha /2) = -\tan (\alpha /2) = \tan (180° - \alpha /2).$

This means that $\angle AEO = \alpha /2.$ In the right $\Delta AOE,$ $EO = r / \tan (\alpha /2).$

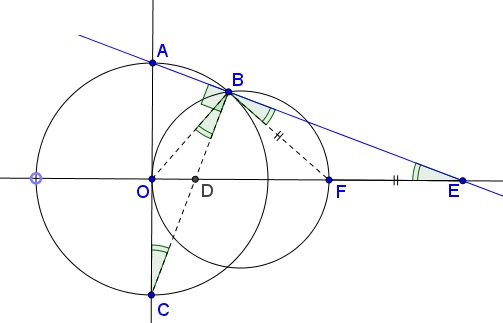
two circles and the limit, proof 5

But $r$ is a function of $\alpha - r = r\alpha$ - which can be determined from the stationary circle. Join $B$ to $F,$ the second end of the diameter. $\Delta OBF$ is right, $OF = 6$, and $\angle OFB = \alpha .$ It follows that $r = OB = 6 \sin (\alpha ).$

Of course we also have

$EO = r / \tan (\alpha /2) = 6 \sin (\alpha ) / \tan (\alpha /2) = 12 \cos ^{2}(\alpha /2).$

Clearly $\alpha$ and $r$ tend to $0$ simultaneously. So, as $r$ tends to $0,$ $\cos ^{2}(\alpha /2)$ tends to $1,$ while $EO$ has the limit of $12.$

Note

Patrick Honner came up with a different opening for the proof.

Let $X$ be the center of the stationary circle. $\Delta ABX$ is isosceles and $OX = BX = 3$, $OB = r.$ Relative to that circle, $\angle AOB$ is bounded by a tangent and a chord, $OB,$ that subtends the central angle $OXB.$ Therefore, $\angle OXB = 2\alpha .$ Dropping a perpendicular from $X$ onto $OB,$ we immediately obtain $OB/2 = 3\sin (\alpha ),$ or $r = 6 \sin (\alpha ).$

Limits in Geometry

71543915

Two Circles and a Limit Trigonometric Solution

Note

Limits in Geometry

Two Circles and a Limit
Trigonometric Solution