Deceptive Appearances
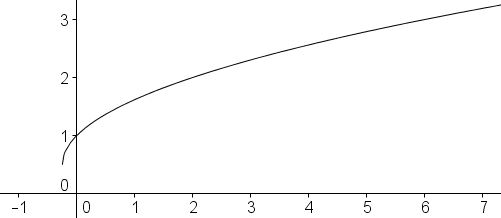
At first sight there is nothing special about the function $\displaystyle y=\frac{1+\sqrt{1+4x}}{2}.$ This is just a slight modification of the common $y=\sqrt{x}.$ Here is the graph of $\displaystyle y=\frac{1+\sqrt{1+4x}}{2}$ which - as a real valued function - is only defined for $x\ge -1/4.$
However, as John Molokach has noticed (I am in John's debt for bringing this to my attention), the function appears under curious circumstances as a limit of a sequence of nested radicals:
$\displaystyle \frac{1+\sqrt{1+4x}}{2}=\sqrt{x+\sqrt{x+\sqrt{x+\ldots}}},$
where the meaning of the ellipsis is revealed through considering a sequence of finite (partial) expressions and proving they have a limit. This was done elsewhere for $x=2,$ with just a claim that the derivation in a general case is rather similar. Similar it is, but not quite, with a relative complication arising for $x\ne 2.$ For the sake of completeness I'll treat here the general case.
For a fixed $x\ge 0,$ define $x_{1}=\sqrt{x},$ and $x_{i+1}=\sqrt{x+x_{i}},$ for $i\ge 1.$ We prove - using the Monotone Convergence Theorem - that so defined sequence has a limit as $i\rightarrow\infty.$
First of all the sequence is not decreasing. Indeed, passing from $x_i$ to $x_{i+1}$ we replace $x$ with $x+\sqrt{x}$, which may not decrease the result: $x_{1}\le x_{2}\le x_{3}\le\ldots$ This part is exactly the same as in case of $x=2.$ To prove the boundedness of the sequence we need to proceed somewhat differently.
Let's try to find an $X$ - an upper bound - such that, $x_{i}\le X$ would imply that also $x_{i+1}\le X.$ Looking at the graph above, suggests that $X=x+1$ may serve our needs. This will be proved by induction.
For any $x\ge 0,$ $\sqrt{x}\le x+1.$ Indeed, for $x\le 1,$ $\sqrt{x}\le 1\le x+1.$ And, for $x\gt 1,$ $\sqrt{x}\lt x\lt x+1.$ This shows that, for $x\ge 0,$ $x_{1}\le x+1.$
Assume that, for some $k\ge 1,$ $x_{k}\le x+1,$ and prove that this implies the inequality $x_{k+1}\le x+1.$ Since the terms of the sequence are all non-negative, the required inequality can be squared:
$\displaystyle x^{2}_{k+1}=x+x_{k}\le x+(x+1)\le 2x+1.$
But, for $x\ge 0,$ $2x+1\le (x+1)^{2},$ because $(x+1)^{2}=x^{2}+2x+1\ge 2x+1.$ Thus, by transitivity, $x^{2}_{k+1}\le 2x+1\le (x+1)^{2},$ which amounts to the required $x_{k+1}\le x+1.$ Thus the sequence $\{x_{i}\}$ is monotone and bounded and, therefore, has a limit, say $L(x),$ which is denoted as $L(x)=\displaystyle\sqrt{x+\sqrt{x+\sqrt{x+\ldots}}}.$ Obviously, $L$ satisfies the equation
$\displaystyle L(x)=\sqrt{x+L(x)},$
solving which gives exactly the formula $\displaystyle L(x)=\frac{1+\sqrt{1+4x}}{2}.$
It appears that we are done. In fact, we are almost done. This is to John Molokach's credit that he noticed a flaw in the above derivation. Before proceeding, could you locate a little something that is not quite correct?
A mistake was committed at the very last step. For $x=0,$ all the terms of the sequence $\{{x_i}\}$ are identically zero. So there is no question about it's having a limit - which is naturally $0$ - in this case. However, $L(0)=1$ which shows that $x=0$ is a special case. What can be made of it?
On one hand, the situations can be exploited to serve a proof (an invalid one, of course) that $0=1.$ Actually, this would be a fallacy more than an invalid proof.
On the other hand, $\displaystyle f(x)=\lim_{n\rightarrow\infty}\sqrt{x+\sqrt{x+\ldots\sqrt{x}}},$ where $n$ is the number of the radicals, can be looked at as a naturally discontinuous function. In particular, it is piecewise defined and could not be represented by a single elementary formula. It could be used as an example to dispel the common conviction that is often created in beginning calculus classes that defining functions by algebraic formulas is germane to the notion of function.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73581257
