Two Circles and a Limit
Proof #1

Barbeau, Klamkin, Moser

We are solving the Two Circles and a Limit problem:

A stationary circle of radius $3$ is centered at $(3, 0).$ Another circle of variable radius $r$ is centered at the origin and meets the positive $y-axis$ in point $A.$ Let $B$ be the common point of the two circles in the upper half-plane. Let $E$ be the intersection of $AB,$ extended, with the $x-axis.$ What happens to $E$ as $r$ grows smaller and smaller?

The notations in the proof are as follows: $C$ is the lowest point of the shrinking circle, $D$ is the intersection of $BC$ with the $x-axis,$ $F$ is the rightmost point of the stationary circle.

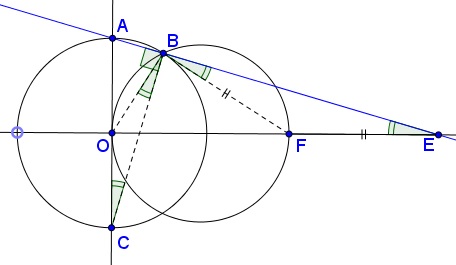
two circles and the limit, proof 1

Since $AC$ is the diameter of the shrinking circle, $\angle ABC$ is right, an so is $\angle DBE.$ Subtracting from both $\angle DBF$ we obtain that

$\angle OBC = \angle FBE.$

Of course we also have

$\angle OBC = \angle OCB.$

On the other hand, $\angle AOB$ is formed by a tangent to and a chord of the stationary circle. Therefore,

$\angle AOB = \angle BFO.$

By the Exterior Angle Theorem,

$\angle AOB = \angle OBC + \angle OCB,$ whereas
$\angle BFO = \angle FBE + \angle FEB.$

From which we conclude that

$\angle FEB = \angle FBE.$

As a consequence,

$FE = FB.$

As $r$ goes to zero, $B$ approaches the origin $O,$ $FB$ approached the diameter $OF.$ Thus $E$ goes to the point twice as far from he origin as $F.$ Note that, since $\Delta DBE$ is right and $FB = FE,$ $F$ serves as the circumcenter of the triangle. So that we also have $FD = FB$ and, by transitivity, $FD = FE.$ $F$ is the midpoint of $DE!$

References

E. J. Barbeau, M. S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges, MAA, 1995, #396
J. Konhauser, D. Velleman, S. Wagon, Which Way Did the Bicycle Go?, MAA, 1996, #5

Limits in Geometry

71547376

Two Circles and a Limit Proof #1

Barbeau, Klamkin, Moser

References

Limits in Geometry

Two Circles and a Limit
Proof #1