Problem 4010 from Crux Mathematicorum
Problem

Solution 1
$\displaystyle\begin{align}&\int_{0}^{\frac{\pi}{2}}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)^{2n}f(x)dx\\ &\qquad=\int_{0}^{\frac{\pi}{4}}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)^{2n}f(x)dx+\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)^{2n}f(x)dx\\ &\qquad=\int_{0}^{\frac{\pi}{4}}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)^{2n}f(x)dx+\int_{0}^{\frac{\pi}{4}}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)^{2n}f(\frac{\pi}{2}-x)dx\\ &\qquad=\int_{0}^{\frac{\pi}{4}}\left[f(x)+f\left(\frac{\pi}{2}-x\right)\right]\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)^{2n}dx. \end{align}$
Note that $\displaystyle \frac{\cos x-\sin x}{\cos x+\sin x}=\tan\left(\frac{\pi}{4}-x\right),\,$ for $\displaystyle x\in \left[0,\frac{\pi}{4}\right],\,$ in particular, implying
$\displaystyle\begin{align}&\int_{0}^{\frac{\pi}{4}}\left[f(x)+f\left(\frac{\pi}{2}-x\right)\right]\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)^{2n}dx\\ &\qquad =\int_{0}^{\frac{\pi}{4}}\left[f(x)+f\left(\frac{\pi}{2}-x\right)\right]\tan^{2n}\left(\frac{\pi}{4}-x\right)dx. \end{align}$
Now, the substitution $\displaystyle \tan\left(\frac{\pi}{4}-x\right)\rightarrow x,\,$ leads to
$\displaystyle\begin{align} &\int_{0}^{\frac{\pi}{4}}\left[f(x)+f\left(\frac{\pi}{2}-x\right)\right]\tan^{2n}\left(\frac{\pi}{4}-x\right)dx\\ &\qquad\int_{0}^{1}x^{2n}\cdot\frac{\displaystyle f\left(\frac{\pi}{4}+\arctan x\right)+f\left(\frac{\pi}{4}-\arctan x\right)}{1+x^2}dx. \end{align}$
To continue,
$\displaystyle \begin{align} &\int_{0}^{\frac{\pi}{2}}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)^{2n}f(x)dx\\ &\qquad 2n\int_{0}^{1}x^{2n}\cdot\frac{\displaystyle f\left(\frac{\pi}{4}+\arctan x\right)+f\left(\frac{\pi}{4}-\arctan x\right)}{2(1+x^2)}dx. \end{align}$
It's well known that for $g\in C[0,1],\,$ $\displaystyle \lim_{t\rightarrow\infty} t\int_0^1x^tg(x)dx=g(1).\,$ It follows that
$\displaystyle \begin{align} &\lim_{n\rightarrow\infty}2n \int_{0}^{1}x^{2n}\cdot \frac{\displaystyle f\left(\frac{\pi}{4}+\arctan x\right)+\left(\frac{\pi}{4}-\arctan x\right)}{2(1+x^2)}dx\\ &\qquad =\frac{1}{4}\left[f(0)+f\left(\frac{\pi}{2}\right)\right], \end{align}$
which is the required limit.
Solution 2
Let $g(x)=f(\pi/2-x)\,$ and
$\displaystyle t(x)=\left(\frac{\cos x - \sin x}{\cos x + \sin x}\right)^2.$
Also, let $\pi/4 = Nh\,$ where $h \ll 1\,$ and $N \gg 1.\,$ Noting that $t(\pi/2-x)=t(x),$
$\displaystyle \begin{align} I &= \lim_{n\to\infty} n\int_{0}^{\pi/2} [t(x)]^nf(x) dx \\ &= \lim_{n\to\infty} n\int_{0}^{\pi/4} [t(x)]^n[f(x)+g(x)] dx \\ &= \sum_{k=1}^{N}\lim_{n\to\infty} n\int_{(k-1)h}^{kh} [t(x)]^n[f(x)+g(x)] dx \end{align}$
Note, for $x\in[0,\pi/4],\,$ $t(0)=1\,$ and $1>t(x)\geq 0\,$ elsewhere. Thus, only the first term in the summation term is non-zero. For, any term other than the first, let $T\,$ and $F\,$ be respectively the upper bounds on the absolute values of $t(x)\,$ and $f(x)\,$ over the interval. Then,
$\displaystyle \begin{align} \lim_{n\to\infty} \left| n\int_{(k-1)h}^{kh} [t(x)]^n[f(x)+g(x)] dx \right| &\leq \lim_{n\to\infty} nh T^n F \\ &\leq hF\lim_{n\to\infty} n T^n \\ &= 0. \end{align}$
This is because $0<|T|<1\,$ and the limit goes to $0:$
$\displaystyle \lim_{n\to\infty}nT^n = \lim_{n\to\infty}\frac{e^{\ln n}}{e^{n \ln (1/T)}} = 0,$
as the polynomial term grows faster than the logarithmic term. Consider the Taylor series expansion of $t(x)\,$ around $x=0\,$ over $x\in[0,h]:$
$t(x)=1-4x+O(x^2).$
The error bound given by
$\displaystyle |t(x)-1+4x| \leq h^2\frac{\max(|t''(x)|)}{2},$
(with the \maximum of the interval considered) goes to zero faster than $h\,$ as $h\rightarrow 0.\,$ Thus, for small $h,\,$ the integral can be written as
$\displaystyle I=\lim_{n\to\infty} n\int_{0}^{h} (1-4x)^n[f(x)+g(x)] dx.$
From the continuity of $p(x)=f(x)+g(x),\,$ for any $\epsilon\,$ there exists $\delta\,$ such that ($|x|\lt \delta) \Rightarrow (p(0)-\epsilon < p(x) \lt p(0)+\epsilon).\,$ For a fixed $\epsilon,\,$ we will choose an $h\,$ (still satisfying the earlier requirements) that is smaller than $\delta.\,$ Noting that $t(x)^n\,$ and also its approximation $(1-4x)^n\,$ is non-negative,
$\displaystyle\begin{align} &(p(0)-\epsilon) \lim_{n\to\infty} n\int_{0}^{h} (1-4x)^n dx \lt I \lt (p(0)+\epsilon) \lim_{n\to\infty} n\int_{0}^{h} (1-4x)^n dx \\ &(p(0)-\epsilon) \lim_{n\to\infty} \left[\frac{1-(1-4h)^{n+1}}{4+4/n}\right] \leq I\leq (p(0)+\epsilon) \lim_{n\to\infty} \left[\frac{1-(1-4h)^{n+1}}{4+4/n}\right] \end{align}$
By the choice of $h,\,$ $1 > (1-4h) > 0.\,$ Thus, the limit term is equal to $\displaystyle \frac{1}{4}.\,$
$\displaystyle \frac{p(0)-\epsilon}{4} \leq I \leq \frac{p(0)+\epsilon}{4}.$
The argument holds for any choice of $\epsilon\,$ however small. Thus,
$\displaystyle I=\frac{p(0)}{4}=\frac{f(0)+f(\pi/2)}{4}.$
Solution 3

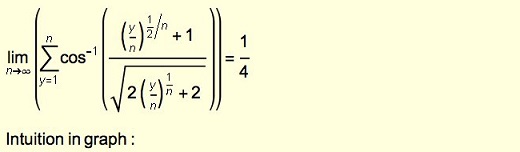
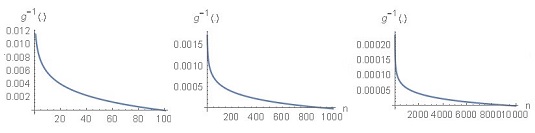
Solution 4
We observe that, if $\displaystyle t(x)=\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)^2=\frac{1-\sin 2x}{1+\sin 2x},\,$ then $\displaystyle t:\,\left[0,\frac{\pi}{2}\right]\rightarrow [0,1]\,$ and $\displaystyle t\in C^1\left[0,\frac{\pi}{2}\right].\,$ Next, note that if $f(x)\,$ is in $\displaystyle C^2\left[0,\frac{\pi}{2}\right],\,$ then we can write
$\displaystyle\begin{align} \lim_{n\rightarrow\infty}n\int_{0}^{\frac{\pi}{2}}t^nf(x)dx&=\lim_{n\rightarrow\infty}\int_{0}^{\frac{\pi}{2}}nt^{n-1}t'(x)\frac{f(x)}{t'(x)}dx\\ &=\lim_{\rightarrow\infty}\left[t(x)\frac{f(x)}{t'(x)}\right]_{0}^{\frac{\pi}{2}}-\lim_{n\rightarrow\infty}n\int_{0}^{\frac{\pi}{2}}t^n(x)\left(\frac{f(x)}{t'(x)}\right)'dx\\ &=\frac{\displaystyle f\left(\frac{\pi}{2}\right)}{\displaystyle t'\left(\frac{\pi}{2}\right)}-\frac{f(0)}{t'(0)}-0, \end{align}$
because $\displaystyle \lim_{n\rightarrow\infty}\int_{0}^{\frac{\pi}{2}}t^n(x)\left(\frac{f(x)}{t'(x)}\right)'dx=0.\,$ But
$\displaystyle t'(x)=-\frac{2\cos 2x}{1+\sin 2x}-\frac{(1-\sin 2x)\cdot 2\cos 2x}{(1+\sin 2x)^2}$
such that,
$\displaystyle \lim_{n\rightarrow\infty}n\int_{0}^{\frac{\pi}{2}}t^nf(x)dx=\frac{\displaystyle f\left(\frac{\pi}{2}\right)}{4}+\frac{f(0)}{4}.$
If $f(x)\,$ is not on $C^2\displaystyle \left[0,\frac{\pi}{2}\right],\,$ we can find $g(x)\,$ and $h(x)\,$ in $C^2\displaystyle \left[0,\frac{\pi}{2}\right]\,$ such that $g(x)\le f(x)\le h(x)\,$ and $g(0)=f(0)=h(0);\,$ $\displaystyle g\left(\frac{\pi}{2}\right)=f\left(\frac{\pi}{2}\right)=h\left(\frac{\pi}{2}\right),\,$ and apply our approach to $g(x)\,$ and $h(x).$
Acknowledgment
This is Problem 4010 from Crux Mathematicorum, proposed by Ovidiu Furdui with a solution (Solution 1) by Leo Giugiuc. Solution 2 is by Amit Itagi; Solution 3 is by N. N. Taleb; Solution 4 is by Andrea Acquaviva.
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73575156
