Sicherman Dice

According to M. Gardner, Col. George Sicherman of Buffulo was the first to pose and solve the following question:

Is it possible to number the faces of a pair of cubes in a way completely different from that of standard dice so that the cubes can be used in any dice game and all the odds will be exactly the same as they are when standard dice are used?

M. Gardner reported the result in an 1978 issue of Scientific American. Here's Col. Sicherman's two dice:

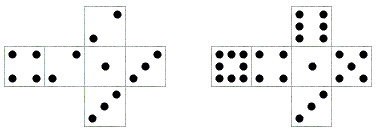
Sicherman dice

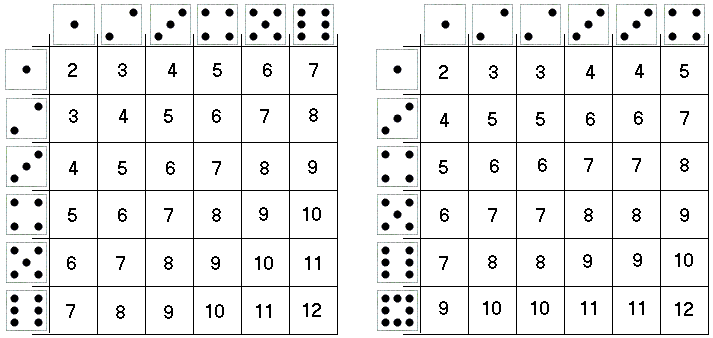
You can compare the two tables of possible outcomes and verify that all integers from 2 through 12 come up with equal frequencies.

Sicherman tables

Broline extended the problem to include m-sided dice, with m not necessarily 6 - dice in the form of Platonic solids - and k ≥ 2, the number of pieces.

Fowler and Swift characterized the sets of numbers (not necessarily 2, 3, ..., 12) that can be realized as the sums of relabeled 6-sided dice with these sums occurring with the usual sum probabilities and gave examples of two dice - with different number of sides - that lead to the same result.

The main tool in these investigations was the probability generating function. Here is the one for a single roll of a die:

f(x) = (1/6)x + (1/6)x² + (1/6)x³ + (1/6)x⁴ + (1/6)x⁵ + (1/6)x⁶.

The exponents indicate possible outcomes; the coefficients the probabilities of the outcomes - all six occur with equal probabilities. For two dice, this expression is squared:

	f²(x)	= [(1/6)x + (1/6)x² + (1/6)x³ + (1/6)x⁴ + (1/6)x⁵ + (1/6)x⁶.]²
		= 6^-2[x² + 2x³ + 3x⁴ + 4x⁵ + 5x⁶ + 6x⁷ + 5x⁸ + 4x⁹ + 3x¹⁰ + 2x¹¹ + x¹²],

and, again, the exponents represent possible outcomes from 2 to 12 that occur with the probabilities given by the coefficients. The coefficients confirm to the count of the outcomes in the left table above.

From the formula for the sum of a geometric progression,

f(x) = (1/6)x(x⁶ - 1)/(x - 1)

= (1/6)x(x³ + 1)(x^{3/^{- 1)/(x - 1)}}

= (1/6)x(x + 1)(x² - x + 1)(x - 1)(x² + x + 1)/(x - 1)

= (1/6)x(x + 1)(x² - x + 1)(x^{2/^{+ x + 1).}}

And, for two dice, we obtain

f²(x) = 6^-2[x(x + 1)(x² - x + 1)(x² + x + 1)]²

= 6^-2g(x)h(x),

where

g(x) = (1/6)x(x + 1)(x² + x + 1) = (1/6)(x⁴ + 2x³ + 2x² + x),

and

h(x) = (1/6)x(x + 1)(x² + x + 1)(x² - x + 1)²

= (1/6)(x⁸ + x⁶ + x⁵ + x⁴ + x³ + x).

These are exactly the generating functions associated with the distribution of numbers on Sicherman's dice:

Sicherman dice

As Col. Sicherman showed, there is no other relabeling of the dice with positive integers that leads to standard probabilities. This can be verified by recombining the factors of the generating function f²(x). The task is straightforward but requires a healthy amount of perseverance.

Reference

D. M. Broline, Renumbering of the Faces of Dice, Mathematics Magazine, Vol. 52, No. 5 (Nov., 1979), pp. 312-315
B. C. Fowler, R. J. Swift, Relabeling Dice, The College Mathematics Journal, Vol. 30, No. 3 (May, 1999), pp. 204-208
M. Gardner, Penrose Tiles to Trapdoor Ciphers, W. H. Freeman and Company, 1989, Ch. 19

41162546