Ceva's Theorem

Giovanni Ceva (1648-1734) proved a theorem bearing his name that is seldom mentioned in Elementary Geometry courses. It's a regrettable fact because not only it unifies several other more fortunate statements but its proof is actually as simple as that of the less general theorems. Additionally, the general approach affords, as is often the case, rich grounds for further meaningful explorations.

27 November 2015, Created with GeoGebra

Ceva's Theorem

In a triangle ABC, three lines AD, BE and CF intersect at a single point K if and only if

(1) AF/FB · BD/DC · CE/EA = 1

(The lines that meet at a point are said to be concurrent.)

Proof 1

Extend the lines BE and CF beyond the triangle until they meet GH, the line through A parallel to BC. There are several pairs of similar triangles: AHF and BCF, AEG and BCE, AGK and BDK, CDK and AHK. From these and in that order we derive the following proportions:

AF/FB = AH/BC (*)
CE/EA = BC/AG (*)
AG/BD = AK/DK
AH/DC = AK/DK

from the last two we conclude that AG/BD = AH/DC and, hence,

BD/DC = AG/AH (*).

Multiplying the identities marked with (*) we get

AF/FB · BD/DC · CE/EA= AH/BC · BC/AG · AG/AH
 = (AH·BC·AG)/(BC·AG·AH)
 = 1

Therefore, if the lines AD, BE and CF intersect at a single point K, the identity (1) does hold. Which is to say that the fact of the three lines intersecting at one point is sufficient for the condition (1) to hold. Let us now prove that it's also necessary. This would constitute the second part of the theorem. In other words, let us prove that if (1) holds then AD, BE, CF are concurrent.

Indeed, assume that K is the point of intersection of BE and CF and draw the line AK until its intersection with BC at a point D'. Then, from the just proven part of the theorem it follows that

AF/FB · BD'/D'C · CE/EA = 1

On the other hand, it's given that

AF/FB · BD/DC · CE/EA = 1

Combining the two we get

BD'/D'C = BD/DC or
BD'/D'C + 1= BD/DC + 1 or
(BD' + D'C)/D'C = (BD + DC)/DC

Finally

BC/D'C = BC/DC

which immediately implies D'C=DC. That is, D' and D are one and the same point.

Q.E.D.

Proof 2

Triangles CKD and BKD have a common altitude hK from K. For their areas we therefore have Area(ΔCKD) = DC·hK/2 and Area(ΔBKD) = BD·hK/2, from which

(2) BD/DC = Area(ΔBKD)/Area(ΔCKD)

Similarly, on considering triangles ACD and ABD,

(3) BD/DC = Area(ΔABD)/Area(ΔACD)

From (2) and (3) we derive

(4) BD/DC = Area(ΔAKB)/Area(ΔAKC)

The latter is a key identity because two similar ones could be written starting with the other two sides:

AF/FB = Area(ΔAKC)/Area(ΔBKC)
CE/EA = Area(ΔBKC)/Area(ΔAKB).

All we need now is to multiply the three identities.

Proof 3

This proof is by Darij Grinberg and appeared at the geometry-college newsgroup. It is also available at his personal site (that since disappeared).

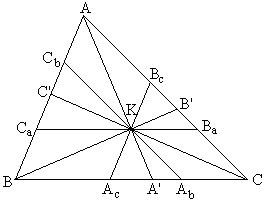
For this proof I changed the notations somewhat. The three lines through the point K are now AA', BB' and CC'. Draw through K three lines -- AcBc||AB, BaCa||BC, and AbCb||AC, as shown in the diagram.

First off, since say, triangles ACC' and BcCK are similar as are triangles BCC' and AcCK, we have

AC'/BcK = CC'/CK, and C'B/KAc = CC'/CK,

which gives

(5) AC'/C'B = BcK/KAc.

From similar triangles ABB' and BcKB' we get

BcK/AB = KB'/BB',

while similarity of triangles ABA' and KAcA' yields

KAc/AB = KA'/AA'.

The latter two identities combine into

BcK/KAc = KB'/KA' : BB'/AA',

or, taking (5) into account,

(6c) AC'/C'B = KB'/KA' : BB'/AA'.

Cyclically, we also have

(6a)BA'/A'C = KC'/KB' : CC'/BB' and
(6b)CB'/B'A = KA'/KC' : AA'/CC'.

The product of the three is the Ceva identity

AC'/C'B · BA'/A'C · CB'/B'A = 1.

Remark 1

Ceva's theorem is the reason lines in a triangle joining a vertex with a point on the opposite side are known as Cevians.

Remark 2

The points D, E, F may lie as well on extensions of the corresponding sides of the triangle, while the point of intersection K of the three cevians may lie outside the triangle. The proof remains the same for all possible configurations as long as all the points involved remain finite. Please look into this circumstance.

Remark 3

The theorem remains valid also if the lines AD, BE and CF are all parallel (in which case it's customary to say that the point K lies at infinity). This case is even simpler than the one just proven. Another exceptional case is when one (or two) of the points D, E, or F is (are) at infinity which means that one of the Cevians is parallel to the side it's supposed to cross. This case too must be treated separately.

Remark 4

An additional proof - a derivation from the 4 Travelers Problem - has been devised by Stuart Anderson.

Corollary 1 (center)

Medians in a triangle intersect at a single point.

Proof

Medians connect vertices with the midpoints of the opposite sides. Therefore, AF/FB = BD/DC = CE/EA = 1. Each of the ratios is 1 and so is their product.

Corollary 2 (incenter)

In a triangle, angle bisectors intersect at a single point.

Proof

For angle bisectors we know that AF/FB = AC/BC, BD/DC = AB/AC, CE/EA = BC/AB. Multiplying the three yields (1).

Corollary 3 (orthocenter)

In a triangle, altitudes intersect at a single point.

Proof

Indeed, right-angled triangles ACD and BCE are similar. Therefore CE/DC = BE/AD. In an analogous manner, AF/EA = CF/BE and BD/FB = AD/CF. Now

AF/FB · BD/DC · CE/EA= CE/DC · AF/EA · BD/FB
 = BE/AD · CF/BE · AD/CF
 = 1.

Remark

It's interesting to compare the direct proofs of the Corollaries with the ones we used for each case separately. Are the latter any easier?

Corollary 4 (Gergonne point)

Let D, E, F be the points where the inscribed circle touches the sides of the triangle ABC. Then the lines AD, BE and CF intersect at one point. (This is known as the Gergonne point, named after Joseph Diaz Gergonne (1771-1859). The ususal notation for the point is Ge.)

Proof

Sides of the triangle being tangent to the inscribed circle, AF = EA, FB = BD, DC = CE so that (1) indeed holds.

(An interactive illustration offers a convincing demonstration of the existence of Gergonne point and of an analogous property of excircles. The proof is virtually the same as in the case of the incircle. Curiously, the concurrency is observed also when one of the vertices of the base triangle is moved to infinity.)

Corollary 5 (Lemoine point)

Symmedians ASa, BSb, CSc intersect at a point (known as the Lemoine point.)

Proof

We'll make use of two ways to compute the area of a triangle. Namely, 2·S = a·b·sin(C) and 2·S = c·hc (and similarly for the other two vertices.) Thus we have

Area(ΔBASa)/Area(ΔAMaC) = BSa/CMa = AB·ASa/AMa·AC
Area(ΔASaC)/Area(ΔAMaB) = CSa/BMa = AC·ASa/AMa·AB

Divide the first of these by the second:

BSa/CMa · BMa/CSa = AB2/AC2

Or, since BMa = CMa,

BSa/CSa = AB2/AC2

Similar identities hold for the other two vertices. All that remains is to multiply the three. (The symmedians have many interesting properties.)

Remark

Corollary 5 actually showed more than it set out to. The result is in fact more general. Let APa, BPb, and CPc be three concurrent Cevians. Reflect the line of APa in the bisector of angle A, and denote the resulting segment as AQa. Construct similarly BQb and CQc as reflections of the other two Cevians. Then the three lines AQa, BQb, and CQc are concurrent.

The lines APa and AQa are isogonal (or isogonal conjugates of each other.) The same is true of the other two pairs. For this reason the two points of concurrency, that of Cevians APa, BPb, and CPc and that of Cevians AQa, BQb, and CQc, are also said to be isogonal conjugates of each other.

Corollary 6

For three concurrent Cevians AD, BE, and CF, if the points D, E, and F are reflected in the midpoints of the corresponding sides, the resulting three lines form another triplet of concurrent Cevians. In other words, isotomic conjugates of concurrent Cevians are also concurrent.

Proof

Indeed, that the given lines are concurrent is reflected by the fact (1) that the product of the three ratios is 1. Now, note that reflection in the midpoint of a side inverts the corresponding ratio. Obviously, the product of the three inverted ratios is still 1.

Corollary 7 (Nagel point)

Let Xa be the point of tangency of side BC and the excircle with center Ia. Similarly define points Xb and Xc on sides AC and AB. Then three lines AXa, BXb and CXc are concurrent.

Proof

Point Xa has a remarkable property of being midway from the vertex A. More accurately, AB + BXa = AC + CXa. Let p be the semiperimeter of ΔABC. Then BXa = p - AB = p - c and CXa = p - AC = p - b. Therefore, BXa/CXa = (p - c)/(p - b). Write the corresponding ratios for side AB and AC and multiply all three equalities to prove the Corollary.

Corollary 8 (R. S. Hu)

Given three nonintersecting mutually external circles, connect the intersections of internal common tangents of each pair of circles with the center of the other circle. Then the resulting three line segments are concurrent.

Created with GeoGebra

Circles B and C are homothetic in D - the point of intersection of their common internal tangents. Which means that BD/DC = rB/rC. Similarly, we have CE/EA = rC/rA and AF/FB = rA/rB.

(See R. B. Nelsen, Proofs Without Words II, MAA, 2000)

Remark

Ceva's theorem is implied by the theorem of Menelaus to which in fact it is equivalent. It also admits a very nice visual proof.

Please try switching to IE 11 (Windows) or Safari (Mac), for no other browser nowadays runs Java applets. If asked whether to allow the applet to load, click Yes - the applet is signed with a security certificate from a trusted company.

What if applet does not run?

Barycenter

The point where three medians of a triangle meet is called the barycenter - the center of gravity - of the triangle. There is a way to justify this designation. Place equal masses w at the vertices of the triangle. Then the midpoint D of BC will be the center of gravity of the vertices B and C. Intuitively, if we place the sum of two masses in their center of gravity then the moment (the mass times the distance) of such a material point relative to any other point will equal the sum of moments of the two original points.

Generally speaking, the center of gravity of two points L with mass wL and M with mass wM is point N with mass wL + wM that satisfies the rule of moments (which is also known as the Law of the Lever): LN·wL = NM·wM and carries the total mass of the two points. We shall adopt the notation

N = Z(L, wL; M, wM)

for the center of gravity (the barycenter) of two material points L and M with masses wL and wM, respectively. (A similar notation applies to the barycenter of any number of points.)

Returning to our case, the center of gravity K of the two points A and D satisfies AK·w = KD·2w or AK = 2KD. It's a well-known feature of the point where the medians meet. The medians are divided in the ratio 1:2 at the point of their intersection. It's interesting to ask a general question: What if the masses we placed at the vertices A, B, C were not equal? The barycenter of the three material points would still exist. Assuming that the barycenter's location is independent of the way it's computed we would actually get a different proof of the Ceva's Theorem.

We wish to demonstrate that the following conditions are equivalent

(1)AF/FB · BD/DC · CE/EA = 1,
(K)AD, BE, CF are concurrent (in, say, K),
(W1)There are wA, wB and wC with pairwise barycenters at D, E, F
(WK)There are wA, wB and wC with the barycenter at K

Ceva's theorem asserts that (1) and (K) are equivalent. (W1) and (WK) are equivalent by the assumption of the independence of the barycenter of calculations, meaning that

  Z(A, wA; B, wB; C, wC)= Z(A, wA; D, wB + wC)
(W) = Z(B, wB; E, wC + wA)
  = Z(C, wC; F, wA + wB).

(1) implies (W1)

Let wA> 0 be arbitrary. Find wB from wAAF = wBFB: wB = wAAF/FB. Next find wC from wBBD = wCDC: wC = wBBD/DC = wA·AF·BD/FB/DC. Now check that also wAEA = wCCE. Indeed,

wCCE = wACE·AF·BD/FB/DC = wAEA

by (1).

(W1) implies (1)

Indeed, if D = Z(B, wB; C, wC) and similarly for E and F, then

 BD/DC= wC/wB,
 CE/EA= wA/wA,
 AF/FB= wB/wC.

Multiplying the three gives (1).

(K) implies (WK)

Find wB and wC as to make D = Z(B, wB; C, wC). Find wA as to make K = Z(A, wA; D, wB + wC). But this makes K (via (W)) the barycenter of the three material points (A, wA), (B, wB), and (C, wC).

Ram Tobolski elucidates: assume (K) holds so that the three segments AD, BE, and CF are concurrent in K. Find (as above), wA, wB, wC as to make D = Z(B, wB; C, wC) and E = Z(C, wC; A, wA). K is the intersection of AD and BE implying that it's the barycenter of (A, wA) and of (D, wB + wC), as well as that of (B, wB) and (E, wC + wA). If F' = Z(A, wA; B, wB) then CF' is concurrent with the barycenter K, i.e., with AD and BE. Because of the uniqueness of CK, F = F'.

(WK) implies (K)

This is a direct consequence of (W). Indeed, by (W), K must lie on each of AD, BE, CF forcing them to be concurrent at K.

As we see, Ceva's theorem (the equivalence of (1) and (K)) is a quintessential expression of the existence of the barycenter of three material points, or (W), without which the barycenter would not be well defined. On the other hand, (W) is a consequence of the linearity of the definitions and can be easily proved in analytic geometry.

Barycenter and Barycentric Coordinates

  1. 3D Quadrilateral - a Coffin Problem
  2. Barycentric Coordinates
  3. Barycentric Coordinates: a Tool
  4. Barycentric Coordinates and Geometric Probability
  5. Ceva's Theorem
  6. Determinants, Area, and Barycentric Coordinates
  7. Maxwell Theorem via the Center of Gravity
  8. Bimedians in a Quadrilateral
  9. Simultaneous Generalization of the Theorems of Ceva and Menelaus
  10. Three glasses puzzle
  11. Van Obel Theorem and Barycentric Coordinates
  12. 1961 IMO, Problem 4. An exercise in barycentric coordinates
  13. Centroids in Polygon
  14. Center of Gravity and Motion of Material Points
  15. Isotomic Reciprocity
  16. An Affine Property of Barycenter
  17. Problem in Direct Similarity
  18. Circles in Barycentric Coordinates
  19. Barycenter of Cevian Triangle
  20. Concurrent Chords in a Circle, Equally Inclined

Menelaus and Ceva

71942568