Stick Broken Into Three Pieces
(Cartesian Coordinates)

Assume a stick is broken at random into three pieces. What is the probability that the pieces can form a triangle?

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

Buy this applet
What if applet does not run?

Explanation

|Contact| |Front page| |Contents| |Probability| |Activities| |Store|

Copyright © 1996-2015 Alexander Bogomolny

Assume two random break points (B1 and B2) are measured from the (lower) end of the stick. Any point P = (P1, P2) inside a square, whose side length is equal to the length of the stick and thought to be 1, represents one such experiment.

With, say, PP1 shorter than PP2, the length of the three pieces are given by

PP1, P1P2 (a shorthand for PP2 - PP1), and 1 - PP2,

and similarly when PP1 > PP2. Three triangle inequalities must be satisfied for the pieces to form a triangle (still assuming PP1 < PP2):

PP1 < P1P2 + (1 - PP2) = 1 - PP1.
P1P2 < PP1 + (1 - PP2) = 1 - P1P2.
1 - PP2 < PP1 + P1P2 = PP2.

which are equivalent to

(1)PP1< 1/2,
(2)PP2 - PP1< 1/2,
(3)1 - PP2< 1/2,

respectively, and similarly when PP1 > PP2.

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

Buy this applet
What if applet does not run?

In the applet, all three are satisfied when P falls inside of one of the pink triangles. This helps solve the problem when the break points are uniformly distributed over the length of the stick. The point P then is uniformly distributed inside the square. The relative area of the pink triangles, which is 1/4, gives the answer in this case.

For the second problem, i.e. where the stick is first broken into two, after which the longer piece is further broken, we have to exclude from consideration the two green triangles, as these correspond to the cases when (probably by accident) the shorter piece gets manhandled and is broken into two. The remaining area is 3/4 of which the two pink triangles with area 1/4 constitute 1/3. However, 1/3 is not the right answer!.

The problem here is in that the second break point may be assumed to be uniformly distributed over the longer piece obtained after the first break up, which is however shorter than the original stick. This means that the point P is no longer distributed uniformly over the square.

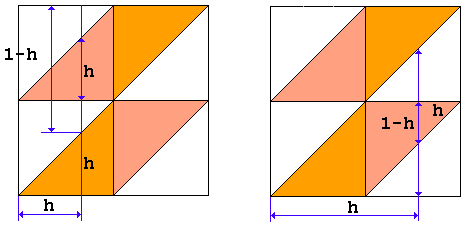
Assume that after breaking the stick into two, the left piece is of length h. If h < 1/2, the probability of P falling into the left pink triangle is h/(1-h) which should be integrated from 0 to 1/2. If h > 1/2, the probability of P falling into the right pink triangle is (1-h)/h which should be integrated from 1/2 to 1. The two integrals are equal (and in fact reduce to each other after a substitution h = 1-h). The sought probability is double their common value of ln(2) - 1/2.

This solution is a slight modification of the one published by J. Whittaker in 1990. I am aware of two other solution that ingeniously cause the probability to be distributed uniformly over the square. Daniel A. Asimov (1996) achieves that by introducing a more problem oriented pair of variables, the Yaglom brothers (1954) make a variable substitution after arriving at the above diagram. Geometrically, the two approaches are slightly different. The more elegant (in my view) solution by D. Asimov is quoted below.

After the first random break, we can (without loss of generality) skip the step of randomly selecting one of the pieces, since the distribution of the left and right pieces will be identical anyway. This simplifies the problem a bit.

Say we always choose the leftmost piece; call its length x.

At this stage we have 2 pieces: [0,x] and [x,1].

Now we want to break [0,x] "at a random point", which amounts to choosing (independent of x) a number y at random in the interval [0,1], where y represents the fraction of x where the break will occur.

So, we end up with 3 pieces: [0,xy], [xy, x], and [x,1]. Their lengths are clearly xy, x-xy = x(1-y), and 1-x.

The distribution on x and y is uniform on the unit square [0,1]×[0,1].

And the region where the 3 pieces form a triangle corresponds to precisely the condition that all 3 sides are of length < 1/2.

The subset of the square, then, where xy < 1/2, x(1-y) < 1/2, and 1-x < 1/2 (i.e. x > 1/2) is the thorn-shaped region bounded on the left by the line x = 1/2 and on the right by the 2 hyperbolas xy = 1/2 and x(1-y) = 1/2.

Calculus then gives the area of this region -- which must be the probability we are seeking -- as Prob(triangle) = ln(2) - 1/2 = .1931471805599453094172321....

References

  1. M. Gardner, The Colossal Book of Mathematics, W. W. Norton & Co, 2001, Ch. 21: Probability and Ambiguity
  2. J. Whittaker, Random Triangles, Am Math Month 97, n 3 (Mar., 1990) pp. 228-230
  3. A. M. Yaglom, I. M. Yaglom , Challenging Mathematical Problems With Elementary Solutions, Holden Day; Rev. edition (June 1, 1964), translated from the 1954 Russian edition

Geometric Probability

|Contact| |Front page| |Contents| |Probability| |Activities| |Store|

Copyright © 1996-2015 Alexander Bogomolny

 49551885

Google
Web CTK