Concurrence Not from School Geometry

Sohail Farhangi
17 February, 2013

Let the incircle \(T\), of \(\Delta ABC\) be tangent to the sides at \(A'\), \(B'\), and \(C'\) as shown below. For a point \(P\) in the plane, let \(A'P\), \(B'P\), and \(C'P\) intersect \(T\) at \(A_1\), \(B_1\), and \(C_1\) respectively. Then \(AA_1\), \(BB_1\), and \(CC_1\) concur at a point \(P'\).

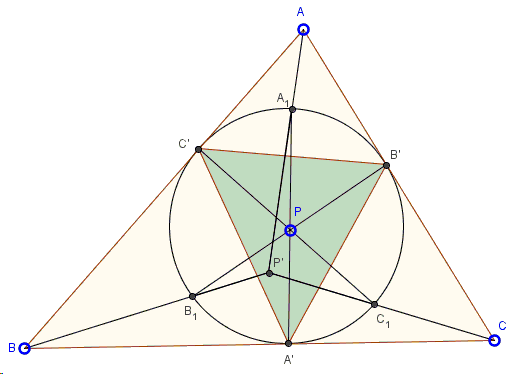
one concurrence involving the incircle and tagential triangle

The applet below serves a dynamic illustration:

Proof

James Tao recommended to me a proof using the trigonometric form of Ceva's Theorem. First we will use the extended Law of Sines on \(\Delta AA_{1}C'\) and \(\Delta A_{1}C'A'\) to obtain the following equations where \(r\) is the radius of \(T\).

(1) \(\displaystyle \frac{C'A_1}{\mbox{sin}(\angle C'AA_{1})}=\frac{AA_1}{\mbox{sin}(\angle AC'A_{1})} \)
(2) \(\displaystyle \frac{C'A_1}{\mbox{sin}(\angle C'A'A_{1})}=2r. \)

Dividing (2) by (1) gives us the following equation:

(3) \(\displaystyle \frac{\mbox{sin}(\angle C'AA_{1})}{\mbox{sin}(\angle C'A'A_{1})}=\frac{2r\mbox{sin}(\angle AC'A_{1})}{AA_{1}}. \)

A similar analysis for \(\Delta AB'A_1\) and \(\Delta A_{1}1B'A'\) will give us the next equation:
(4) \(\displaystyle \frac{\mbox{sin}(\angle B'AA_{1})}{\mbox{sin}(\angle B'A'A_{1})}=\frac{2r\mbox{sin}(\angle AB'A_{1})}{AA_{1}}. \)

Now dividing (3) by (4) yields another equation:

(5) \(\displaystyle \frac{\mbox{sin}(\angle C'AA_{1})\mbox{sin}(\angle B'A'A_{1})}{\mbox{sin}(\angle C'A'A_{1})\mbox{sin}(\angle B'AA_{1})}=\frac{\mbox{sin}(\angle AC'A_{1})}{\mbox{sin}(\angle AB'A_{1})}. \)

Now note that \(\angle AB'A_{1}=\angle B'A'A_1\) since \(AB'\) is tangent to \(T\), and similarly we have \angle \(AC'A_{1} = \angle C'A'A_1\), which gives us

(6) \(\displaystyle \frac{\mbox{sin}(\angle C'AA_{1})}{\mbox{sin}(\angle B'AA_{1})}=\bigg(\frac{\mbox{sin}(\angle C'A'A_{1})}{\mbox{sin}(\angle B'A'A_{1})}\bigg)^{2}. \)

Finally, we are ready to apply the trigonometric form of (the inverse of) Ceva's theorem:

(7) \(\displaystyle \frac{\mbox{sin}(\angle C'AA_{1})\mbox{sin}(\angle B'CC_{1})\mbox{sin}(\angle A'BB_{1})}{\mbox{sin}(\angle A_{1}AB')\mbox{sin}(\angle C_{1}CA')\mbox{sin}(\angle B_{1}BC')}= \\ \displaystyle\bigg(\frac{\mbox{sin}(\angle PA'C')\mbox{sin}(\angle PC'B')\mbox{sin}(\angle PB'A')}{\mbox{sin}(\angle B'A'P)\mbox{sin}(\angle A'C'P)\mbox{sin}(\angle C'B'P)}\bigg)^{2}=1. \)

Menelaus and Ceva

72352941