Archimedes' Law of the Lever
Archimedes' Law of the Lever, i.e. the statement about balancing a beam with different weights distributed along its length, is a classical example of a problem drawn from and applied in, the physical world but which is most illuminated when treated in abstract mathematical terms. The great Archimedes (c. 287-212 BC) was the first to give such treatment in one of his surviving works. Following in footsteps of Euclid, Archimedes sets up a few axioms which are simple abstractions of the everyday experience and from which he proceeds to derive step-by-step the less obvious properties. He is concerned with the situation where the beam is supported at a point (known as a fulcrum) from which the distances to the weights are measured. The center of gravity of several weights placed on the beam is exactly the fulcrum for which the beam is horizontal, i.e. is in equilibrium.
To give you the flavor of the work, [Archimedes, p. 502] starts thus:
I postulate the following:
- Equal weights at equal distances are in equilibrium, and equal weights at unequal distances are not in equilibrium but incline towards the weight which is at the greater distance.
- If, when weights at certain distances are in equilibrium, something is added to one of the weights, they are not in equilibrium but incline towards that weight to which the addition was made.
- Similarly, if anything is taken away from one of the weights, they are not in equilibrium but incline towards the weight from which nothing was taken.
- When equal and similar plane figures coincide if applied to one another, there centers of gravity similarly coincide.
Proposition 1
Weights that balance at equal distances are equal.
For, if they are not equal, take away from the greater the difference between the two. The remainder then will not balance [Post. 3]; which is absurd [Post. 1]. Therefore the weights cannot be unequal.
Proposition 2
Unequal weights at equal distances will not balance but will incline towards the greater weight.
For take away from the greater the difference between the two. The equal remainders will therefore balance [Post. 1] Hence, if we add the difference again, the weights will not balance but incline towards the greater [Post. 2].
Proposition 3
Unequal weights will balance at unequal distances, the greater weight being at the lesser distance.
Let A, B be two unequal weights (of which A is the greater) balancing about C at distances AB, BC respectively.
Then AC be less than CB. For, if not, take away from A the weight
Hence, AC < CB. Conversely, if the weights balance, and
What we are concerned with here are the Law of the Lever, as expressed in Propositions 6 and 7:
Propositions 6, 7
Two magnitudes, whether commensurable [Prop. 6] or incommensurable [Prop. 7], balance at distances reciprocally proportional to the magnitudes.
The applet below illustrates the proof of Proposition 6, i.e. the case where two weights can be measured in terms of a common unit measure. The applet follows the modern rendition of the proof from [Stein and Hirshfeld].
Given two unequal weights - 3 and 4 at the beginning, but these can be changed by clicking at the two numbers at the bottom of the applet.

Replace each with an equivalent number of unit weights and place them so as to preserve the center of gravity of the two given weights. For 3 this means placing one unit at the same point and two other units on both sides and at equal distances from there.
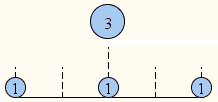
For 4 this means placing two units on each side.
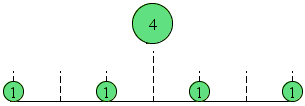
Subject to this requirements, the unit weights could be placed arbitrarily. For the sake of the proof, their distribution over the beam needs to be uniform.

To achieve the uniformity, the segment between the initial weights (of 3 and 4) needs to be divided into 7 equal pieces and a few pieces of the same length need to be added on both sides of the beam. The result is seven unit weights with three sharing the center of gravity of the weight 3 and the other four sharing the center of gravity with the weight 4. The seven unit weights have the center of gravity at the midpoint between the extremes, i.e., at the location of the middle unit weight. Placing a fulcrum at this point will balance the system of 7 weights and also the system of the two initial weights of 3 and 4 units. This point divides the beam in the ratio of 4:3.
| What if applet does not run? |
Note that at times it is possible to find several common units for the given two weights. For example, for weights 6 and 8 we could choose either 1 or 2 as a common unit. In the first case, the fulcrum will be located at the point that divides the beam in ratio 8:6; in the second 4:3, which is one and the same point. The situation repeats itself every time the given integer weights are not mutually prime, i.e. have a non-trivial (greater than 1) common factor. The applet allows you to pick the largest possible - the greatest common divisor of the two integer weights.
The Law of Lever is easily extended to the case of rational weights as two fractions are always commensurable. Given two fractions p/q and r/s,
To prove his Proposition 7, i.e., the case where the two given weights are incommensurable, Archimedes makes an implicit assumption that each is arbitrary close to a magnitude commensurable with the other. As we now know this is of course true. This follows from the density of the rational numbers among all reals (and relevant here is an application of the Pigeonhole principle).
Assume two incommensurable weights U an V located at points A and B are not balanced at point C satisfying
References
- S. Stein, Archimedes: What Did He Do Besides Cry Eureka?, MAA, 1999
- A. Hirshfeld, Eureka Man: The Life and Legacy of Archimedes, Walker & Company, 2009
- Archimedes, On the Equilibrium of Planes or The Centers of Gravity of Planes I, Great Books of the Western World, v 11, Britannica, 1952, pp. 502-509
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73508486
