Two Triangles Inscribed in a Conic - with Elementary Solution

Jack D'Aurizio

The following ideas come from Gabriel Giorgieri, and I am grateful to him. (The theorem below constitutes the statement suggested by Vladimir Nikolin and generalized by Hubert Shutrick.)

Assume that two triangles \(ABC\) and \(DEF\) are inscribed in the same conic and intersect in six points \(G,H,I,J,K,L.\)

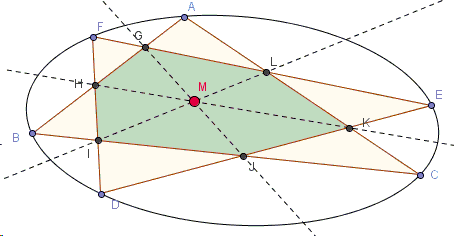
wo triangles inscribed in a conic

Then the lines \(GJ\), \(HK\), \(IL\) are concurrent.

(The applet below illustrates the proof. Points \(A\), \(B\), \(C\), \(D\), \(E\), \(F\) are draggable.)

Proof

Without loss of generality, we can assume that the circumscribed conic is a circle. If we call \(X\) the intersection of \(CF\) and \(BE,\) \(Y\) the intersection of \(AD\) and \(CF,\) \(Z\) the intersection of \(AD\) and \(BE,\) by the Pascal theorem we know that \(G,\) \(Y,\) \(J\) are aligned, and the same holds for \(H,\) \(X,\) \(K,\) and \(I,\) \(Z,\) \(L.\) So we only need to prove that \(GY,\) \(HX,\) \(IZ\) are concurrent cevians with respect to the triangle \(XYZ\).

the lines joining the opposite points of intersection of the sides of two triangles inscribed in a conic concur in a point

In order to apply the Trig Ceva theorem, we express the ratio \(\displaystyle\frac{\mbox{sin}(ZXK)}{\mbox{sin}(KXY)}\) by exploiting the fact that in \(\Delta BFX\) the cevians \(KX,\) \(AB,\) \(DF\) concur in \(H.\) What we get is:

\(\displaystyle \begin{align} \frac{\mbox{sin}(ZXK)}{\mbox{sin}(KXY)} &= \frac{\mbox{sin}(HXB)}{\mbox{sin}(HXF)} \\ &= \frac{\mbox{sin}(BFH)}{\mbox{sin}(HFX)} \cdot \frac{\mbox{sin}(HBX)}{\mbox{sin}(HBF)}, \end{align} \)

so, by denoting with \([UV]\) the sine of half the angle between \(U\) and \(V\) in the circumcircle of \(\Delta ABC,\) we get:

\(\displaystyle \frac{\mbox{sin}(ZXK)}{\mbox{sin}(KXY)} = \frac{[BD]}{[CD]} \cdot \frac{[AE]}{[AF]}, \)

and, in the same way:

\( \displaystyle\frac{\mbox{sin}(XYG)}{\mbox{sin}(GYZ)} = \frac{[CE]}{[AE]} \cdot \frac{[BF]}{[BD]}, \\ \displaystyle\frac{\mbox{sin}(YZI)}{\mbox{sin}(IZX)} = \frac{[AF]}{[BF]}\cdot \frac{[CD]}{[CE]}. \)

The product of the last three right-hand sides is one, proving that the lines \(XK,\) \(YG,\) \(ZI\) are concurrent, QED.

As already noted, this concurrence of Pascal lines is different from the ones stated by Steiner and Kirkman. This theorem should have a proper name! :)

Menelaus and Ceva

72347967