Problem in Direct Similarity

What Might This Be About?

Source

The problem below grew out from an observation by Miguel Ochoa Sanchez:

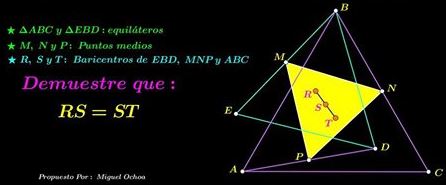
Problem in Direct Similarity, original

Problem

Let $ABC$ and $EBD$ be two similar triangles $M,N,P$ the midpoints of $BE,BC,AD,$ respectively. Define $R,S,T$ as the barycenters of triangles $EBD,MNP,ABC.$

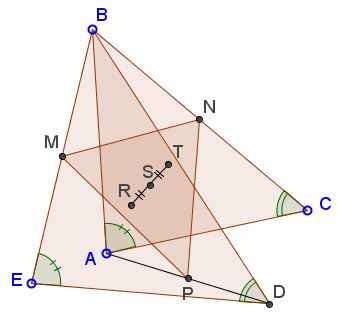
Problem in Direct Similarity, problem

Then $R+T=2S.$

Proof

We'll see the problem as set in affine geometry.

Let $B = 0,$ the origin, $E = x,$ $D = y,$ $a$ - spiral similarity around $B$ s.t. $A = ax,$ $C = ay.$ Then $M = x/2,$ $N = $ay/2,$ $P = (ax + y)/2.$

Further, $R = (x+y)/3,$ $T = (ax+ay)/3,$

$S = (x/2+ay/2+ (ax + y)/2)/3=((x+y)/3+(ax+ay)/3)/2=(R+T)/2.$

Note that $\Delta MNP$ is not similar to $\Delta ABC.$ Using complex numbers, Leo Giugiuc proved that if $ABC$ and $EBD$ are equilateral then so is $MNP;$ and Gregoire Nicollier showed that $MNP$ and $EBD$ are directly similar if and only if $EBD$ is equilateral.

Acknowledgment

The original statement has been posted by Leo Giugiuc at the CutTheKnotMath facebook page with credits to Miguel Ochoa Sanchez.

Barycenter and Barycentric Coordinates

  1. 3D Quadrilateral - a Coffin Problem
  2. Barycentric Coordinates
  3. Barycentric Coordinates: a Tool
  4. Barycentric Coordinates and Geometric Probability
  5. Ceva's Theorem
  6. Determinants, Area, and Barycentric Coordinates
  7. Maxwell Theorem via the Center of Gravity
  8. Bimedians in a Quadrilateral
  9. Simultaneous Generalization of the Theorems of Ceva and Menelaus
  10. Three glasses puzzle
  11. Van Obel Theorem and Barycentric Coordinates
  12. 1961 IMO, Problem 4. An exercise in barycentric coordinates
  13. Centroids in Polygon
  14. Center of Gravity and Motion of Material Points
  15. Isotomic Reciprocity
  16. An Affine Property of Barycenter
  17. Problem in Direct Similarity
  18. Circles in Barycentric Coordinates
  19. Barycenter of Cevian Triangle
  20. Concurrent Chords in a Circle, Equally Inclined

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

71878393