Cevian Cradle II
What is this about?
Problem
Let $P$ be a point in the plane of $\Delta ABC$ and $AA',$ $BB',$ and $CC'$ the corresponding cevians. Let $A_0,$ $B_0,$ $C_0,$ $A_1,$ $B_1,$ $C_1,$ be the midpoints of $BC,$ $AC$, $AB,$ $B'C',$ $A'C'$, $A'B',$ respectively.
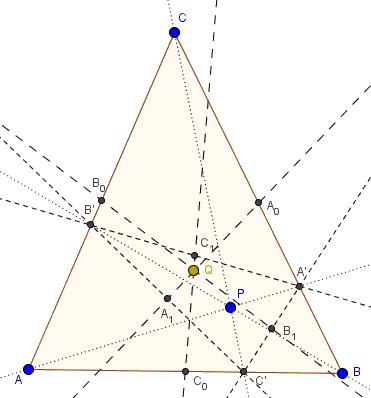
Prove that $A_0A_1,$ $B_0B_1,$ and $C_0C_1$ are concurrent.
Hint
This is probably inevitable to apply one way or another Ceva's theorem. It also appear useful to look into barycentric coordinates. But most direct application comes from what is known as Cevian nest.
Note also that there is a more verbose formulation that seems rather suggestive of the nature of the problem:
The medial triangle of a cevian triangle is perspective with the medial triangle of the reference triangle.
Solution
Elsewhere we proved that a cevian triangle of a cevian triangle is perspective to the base triangle. I am sure the two problems are related and there is a shortcut to solving the current one via the former. I am looking for that shortcut. Meanwhile, there's a more straightforward solution.
Assume point $P$ has barycentric coordinates $(\alpha ,\beta ,\gamma),$ $\alpha +\beta +\gamma =1.$(When the coordinates are merely homogeneous I shall omit the parentheses and replace commas with semicolons.) Points $A',B',C'$ have coordinates $0:\beta :\gamma,$ $\alpha :0:\gamma,$ and $\alpha :\beta :0.$ We can also write, for example, $A'=(0,\beta/(\beta +\gamma),\gamma /(\beta +\gamma)).$ We further have $A_0(0,1/2,1/2),$ $B_0(1/2,0,1/2),$ and $C_0(1/2,1/2,0).$

Now,
\(\displaystyle \begin{align} A_1 &= \frac{1}{2}(\frac{\alpha}{\alpha+\gamma}+\frac{\alpha}{\alpha+\beta}, \frac{\beta}{\alpha+\beta},\frac{\gamma}{\alpha+\gamma}) \\ &= \alpha (2\alpha +\beta +\gamma) :\beta (\alpha +\gamma ):\gamma (\alpha +\beta ). \end{align} \)
$B'$ and $C'$ are expressed similarly. Line $AA'$ is best defined by a determinant equation:
\(\displaystyle \left|\begin{array}{ccc} x & y & z \\ \alpha (2\alpha +\beta +\gamma) & \beta (\alpha +\gamma ) & \gamma (\alpha +\beta ) \\ 0 & 1 & 1 \end{array}\right| =0, \)
which, when expanded, translates into
$AA':$ $\alpha (\beta -\gamma )x-\alpha (2\alpha +\beta +\gamma) y+\alpha (2\alpha +\beta +\gamma) z = 0.$
Similarly,
$BB':$ $\beta (\alpha +2\beta +\gamma )x +\beta (\gamma -\alpha) y-\beta (\alpha +2\beta +\gamma) z = 0$
and
$CC':$ $-\gamma (\alpha +\beta +2\gamma )x+\gamma (\alpha +\beta +2\gamma ) y+\gamma (\alpha -\beta) z = 0.$
The three lines are concurrent, provided,
\(\displaystyle \left|\begin{array}{ccc} \alpha (\beta -\gamma ) & -\alpha (2\alpha +\beta +\gamma) & \alpha (2\alpha +\beta +\gamma) \\ \beta (\alpha +2\beta +\gamma ) & \beta (\gamma -\alpha) & -\beta (\alpha +2\beta +\gamma) \\ -\gamma (\alpha +\beta +2\gamma ) & \gamma (\alpha +\beta +2\gamma ) & \gamma (\alpha -\beta) \end{array}\right| =0, \)
Well, wolframalpha refused to consider this determinant, leaving me with no choice but to do the calculations by hand. I loath to apply the direct expansion but shall use, instead, a series of simplifying transformations.
So, let's start by separating the common factors in each row and using $\alpha +\beta +\gamma =1:$
\(\displaystyle \alpha\beta\gamma\left|\begin{array}{ccc} \beta -\gamma & -(\alpha +1) & (\alpha +1) \\ (\beta+1 ) & \gamma -\alpha & -(\beta+1) \\ -(\gamma+1) & (\gamma+1) & \alpha -\beta \end{array}\right| =0, \)
which looks more manageable.
If either $\alpha,$ or $\beta,$ or $\gamma$ is $0$ there is nothing to prove. So assume none is. We are left with proving
\(\displaystyle \left|\begin{array}{ccc} \beta -\gamma & -(\alpha +1) & (\alpha +1) \\ (\beta+1 ) & \gamma -\alpha & -(\beta+1) \\ -(\gamma+1) & (\gamma+1) & \alpha -\beta \end{array}\right| =0, \)
Subtracting the last row from the second one seems also to simplify the determinant:
\(\displaystyle \left|\begin{array}{ccc} \beta -\gamma & -(\alpha +1) & (\alpha +1) \\ (\beta+\gamma+2) & -(\alpha +1) & -(\alpha +1) \\ -(\gamma+1) & (\gamma+1) & \alpha -\beta \end{array}\right| =0, \)
Adding the second column to the last:
\(\displaystyle 4\left|\begin{array}{ccc} \beta -\gamma & -(\alpha +1) & 0 \\ (\beta+\gamma+2) & -(\alpha +1) & -(\alpha +1) \\ -(\gamma+1) & (\gamma+1) & \alpha +\gamma \end{array}\right| =0, \)
Removing the factor $4$ and subtracting the first row from the second:
\(\displaystyle \left|\begin{array}{ccc} \beta -\gamma & -(\alpha +1) & 0 \\ 2(\gamma+1) & 0 & -(\alpha +1) \\ -(\gamma+1) & (\gamma+1) & \alpha +\gamma \end{array}\right| =0, \)
Now, let's add the second column to the first:
\(\displaystyle 4\left|\begin{array}{ccc} -(\alpha +\gamma) & -(\alpha +1) & 0 \\ \gamma+1 & 0 & -(\alpha +1) \\ 0 & (\gamma+1) & \alpha +\gamma \end{array}\right| =0, \)
The latter determinant is readily expanded into
\( (\alpha +\gamma)(\alpha +1)(\gamma+1) - (\alpha +\gamma)(\alpha +1)(\gamma+1) = 0, \)
proving the assertion.
I have a nugging feeling that a stronger assertion is true: two triangles having the same barycentric coordinates, one relative to the reference triangle, the other relative to a cevian triangle of the latter, are perspective. This requires further investigation.
Acknowledgment
The problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page. Dao Thanh Oai credits Ta Hong Son (April @ the artofproblemsolving site) with discovering the proposition earlier (2007), see https://www.artofproblemsolving.com/Forum/viewtopic.php?t=150123%3Fml%3D1
Menelaus and Ceva
- The Menelaus Theorem
- Menelaus Theorem: proofs ugly and elegant - A. Einstein's view
- Ceva's Theorem
- Ceva in Circumscribed Quadrilateral
- Ceva's Theorem: A Matter of Appreciation
- Ceva and Menelaus Meet on the Roads
- Menelaus From Ceva
- Menelaus and Ceva Theorems
- Ceva and Menelaus Theorems for Angle Bisectors
- Ceva's Theorem: Proof Without Words
- Cevian Cradle
- Cevian Cradle II
- Cevian Nest
- Cevian Triangle
- An Application of Ceva's Theorem
- Trigonometric Form of Ceva's Theorem
- Two Proofs of Menelaus Theorem
- Simultaneous Generalization of the Theorems of Ceva and Menelaus
- Menelaus from 3D
- Terquem's Theorem
- Cross Points in a Polygon
- Two Cevians and Proportions in a Triangle, II
- Concurrence Not from School Geometry
- Two Triangles Inscribed in a Conic - with Elementary Solution
- From One Collinearity to Another
- Concurrence in Right Triangle

|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73581373
