Ceva in Circumscribed Quadrilateral

 

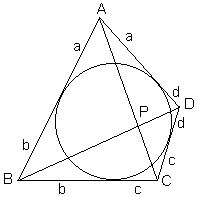
Let ABCD be a quadrilateral circumscribed around a circle. Denote the lengths of tangents from the vertices A, B, C, and D to the circle as a, b, c, d, respectively. Finally, let P be the point of intersection of the diagonals AC and BD. Then we have

(1) AP/PC = a/c.

Proof

Let E be the point of tangency of the incircle on side AB and F be the point of tangency on side BC.

 

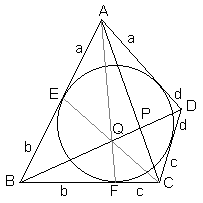
By Brianchon's theorem the lines AF, BP, and CE concur at, say, point Q. Apply Ceva's theorem to ΔABC:

  AP/PC · CF/FB · BE/EA = 1.

In other words,

  AP/PC · c/b · b/a = 1.

And, finally,

  AP/PC = a/c.

Remark

Darij Grinberg has gracefully noted that the theorem has been established by more elementary means elsewhere.

Menelaus and Ceva

72200745