Stick Broken Into Three Pieces
(Trilinear Coordinates)

Assume a stick is broken at random into three pieces. What is the probability that the pieces can form a triangle?

Explanation

Copyright © 1996-2009 Alexander Bogomolny

1. Two break points are selected randomly (and distributed uniformly) on the stick.
2. The stick is first broken into two pieces. The longest (or rather, not the shortest) is then broken into two.
3. The stick is first broken into two pieces. A piece randomly selected with probability 1/2 is then broken into two.
4. The stick is first broken into two pieces. A piece randomly selected with the probability proportional to its length is then broken into two.

In any event, the diagram presented by the applet is helpful in finding the answers.

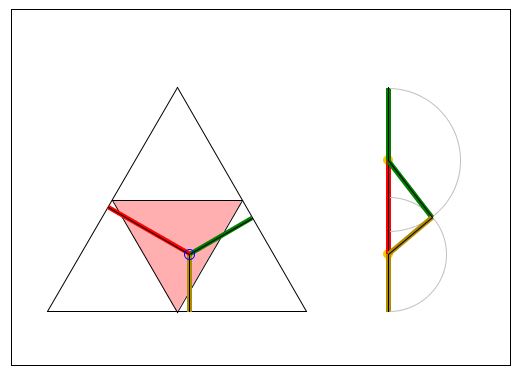
From a point P inside (or on a side) of an equilateral triangle ABC drop perpendiculars PP_a, PP_b, PP_c to its sides. By Viviani's theorem, the sum

is independent of P and is equal to any of the triangle's altitudes. Let's take a triangle whose altitude exactly measures the length of the stick. Connect the midpoints of the sides to split ABC into four equal triangles, with the medial triangle in the middle. Then it is easy to surmise that the three pieces PP_a, PP_b, PP_c form a triangle iff P lies inside the medial triangle. (Otherwise, one of the segments will be longer than half of an altitude, therefore making the sum of the other two shorter than half of an altitude. Thus it is clear that if P does not belong to the medial triangle one of the three triangle inequalities for PP_a, PP_b, PP_c will fail. And the argument is reversible.)

Note also, that point P is uniquely determined by the lengths of the three segments PP_a, PP_b, PP_c. Indeed, the latter may be looked at as the trilinear coordinates of point P.

(For equilateral triangles trilinear coordinates coincide with the barycentrics. In the barycentric coordinates, the first of the above problems alng with a generalization to more than 2 break points has been treated elsewhere.)

With this preliminaries, we may now tackle various formulations of our problem.

1. Two break points are selected randomly on the stick.

   There is 1 in 4 chance that point P falls inside the medial triangle. Point P is uniquely and randomly determined by the two break points. If the points are distributed uniformly and chosen independently, the probability that a triangle can be put together from the three pieces is 1/4.

2. The stick is first broken into two pieces. The longest (or rather, not the shortest) is then broken into two.

   Assume that the shorter piece is represented by the vertical perpendicular to PP_c. Then, as above, P must lie below the vertical edge of the medial triangle. Which means that in this case, in order that the three pieces could form a triangle, P should lie inside of one (still the medial) of the three triangles. This has 1 chance in three with the probability of 1/3.

   Easy, is not it? However, there is a pitfall which is often missed. I have missed it first as did M. Gardner's in a Scientific American article. The article was later included in his collection The Colossal Book of Mathematics (Chapter 21), wherein an Addendum he has corrected the mishap. (M. Gardner also cites a respectable textbook that was also guilty of the same error.)

   The situation now is a little more complicated than in the first problem. Even though the three triangles at hand have equal areas as before, the probability, in this case, is not distributed uniformly over the triangle. This is because the second point is being chosen randomly over a piece shorter than the whole stick, so it can't be thought of as being uniformly distributed over the original length. An observation to this effect has been made by Joe Whittaker in 1990. His reasoning was based on diagrams drawn in Cartesian coordinates and probabilities distributed in a square. (The problem has been also treated in Challenging Mathematical Problems With Elementary Solutions by the Yaglom brothers and in an online discussion.)

   Below, I offer a treatment of the problem based on a triangular diagram.

   

   Assume that after the first break the pieces have lengths h and (1-h), with h < (1-h), i.e. h < 1/2, as expected. With h fixed, we randomlly (and uniformly) break the piece of length (1-h). The probability that the three pieces thus obtained will form a triangle clearly depends on h. It is small if h is small, and it is nearing 1 for h close to 1/2. More accurately, this probability is equal to the ratio VW/UZ, but:

   (*)	VW/UZ = h/(1-h)!

   The total probability is given as the integral of the expression in (*) from 0 to 1/2, i.e., over the range of eligible h:

   The probability we are looking for is the conditional probability obtained under the assumption that h < 1/2. Thus the integral must be divided by 1/2. The result, 2·ln(2) - 1, is approximately equal to 0.386, is slightly more than 1/3, and has been verified experimentally.

   Remark 1

   I am indebted to Orion Elenzil for questioning the original line of reasoning and for drawing my attention to the discrepancy between the original derivation and experimental data.

   Remark 2

   In the addendum to Chapter 21, M. Gardner tells of his own misadventure with the problem. For the Scientific American article, he picked his solution from W. A. Whitworth's DDC Exercises in Choice and Chance, Problem 677. He claims that the same answer could have been found in many other books on probability. A few of his readers pointed out the blunder and sent a correct solution, which has been reported in the addendum.

3. The stick is first broken into two pieces. A piece randomly selected with probability 1/2 is then broken into two.

   If each of the pieces is selected with the probability 1/2, then the total probability of interest is

   1/2·0 + 1/2·(2·ln(2) - 1).

   But what if the probability of selecting one of the two pieces obtained after breaking the stick grows with the length of the piece?

4. The stick is first broken into two pieces. A piece randomly selected with the probability proportional to its length is then broken into two.

   Let, as above, h denote the length of the smaller piece. There is no point in breaking this piece (see, #3.) The probability of selecting the longer piece is now 1-h. (*) has now to be recognised as the conditional probability of the three pieces forming a triangle provided that the length of the longer stick is 1-h. The probability of this event is

   (**)	h/(1-h)·(1-h) = h.

   This ought to be integrated from 0 to 1/2; the result is to be multiplied by 2, which gives the probability of 1/4, as in #1. The result is not entirely unexpected. Indeed, it is not hard to surmise that the two problems (#1 and #4) are just reformulations of each other.

References

1. M. Gardner, The Colossal Book of Mathematics, W. W. Norton & Co, 2001, Ch. 21: Probability and Ambiguity
2. J. Whittaker, Random Triangles, Am Math Month 97, n 3 (Mar., 1990) pp. 228-230
3. A. M. Yaglom, I. M. Yaglom , Challenging Mathematical Problems With Elementary Solutions, Holden Day; Rev. edition (June 1, 1964)

• Barycentric Coordinates and Geometric Probability
• Stick Broken Into Three Pieces (Cartesian Coordinates)
• Stick Broken Into Three Pieces (Trilinear Coordinates)

Copyright © 1996-2009 Alexander Bogomolny