The 2016 ARML Competition, Problem 7
Problem

Solution 1
Using "~" to indicate that a random variable "has a probability density function that follows the tilde,"
$\max(x,y)\;\tilde\;2a,\\ \max(x,y,z)\;\tilde\;3a^2,\,\text{etc}\ldots\;(a\in[0,1]).\\ \text{This means}\;~\; \min(x,y,z)\;\tilde\;3a^2-6a+3.\\ \text{Convolve to get}\, -6a^2+6a.\\ \text{Integrate from}\; 0\rightarrow 2/3.$
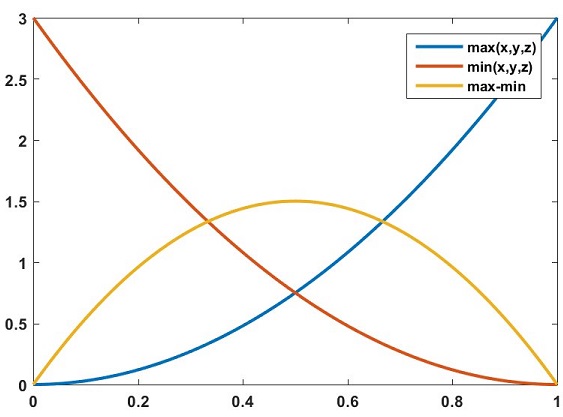
Answer: $0.7407\ldots$
Solution 2
Consider the ordering $x\ge y\ge z.\,$ The probability to be calculated is $3!,$ times the probability for the assumed case. The $3!\,$ comes from permuting the chosen ordering. Thus,
$\displaystyle \begin{align} P&=3!\int_{z=0}^1\int_{y=z}^{\min(1,z+2/3)}\int_{x=y}^{\min(1,z+2/3)}dxdydz\\ &=6\left(\int_{z=0}^{1/3}\int_{y=z}^{z+2/3}\int_{x=y}^{z+2/3}dxdydz+\int_{z=1/3}^1\int_{y=z}^1\int_{x=y}^1dxdydz\right)\\ &=6\left(\frac{2}{27}+\frac{4}{81}\right)\\ &=\frac{20}{27}\approx 0.741 \end{align}$
Solution 3
Let $r=\max(x,y,z)-\min(x,y,z).\,$ The distribution has for pdf $f(w)=3-3(1-w)^2-3w^2\,$ and for cdf $F(w)=3w^2-2w^3.\,$ $\displaystyle F\left(\frac{2}{3}\right)=\frac{20}{27}.$
Expanded Solution 3
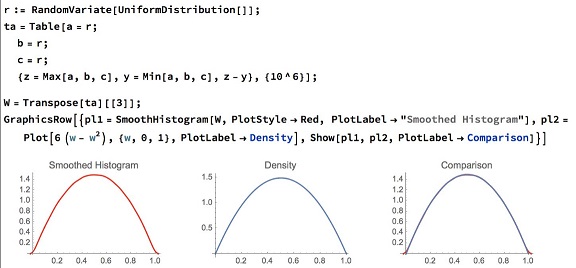
... we will follow three approaches one a formal proof, one an intuitive snap derivation, one a Monte Carlo assessment.
Approach 1
We have 6 permutations of the set $\{x,y,z\},\,$
$\{x\ge y\ge z,\,x\ge z\ge y,\,y\ge x\ge z,\,y\ge z\ge x,\,z\ge x\ge y,\,z\ge y\ge x\}.$
all equiprobable with $\displaystyle \frac{1}{6}\,$ probability. So getting the marginal distribution of the middle in order, defined as $\{y:\,x\ge y\ge z\},\,$ that is, lying between $x\,$ (the max) and $z\,$ (the min) gives us:
$\displaystyle f_y(x\ge y\ge z)=\int_0^1\int_0^1\mathbb{1}_{x\ge y\ge z}dxdz=y-y^2.$
Now the cdf of $W,\,$ i.e., $P(w\gt max-min)\,$ corresponds to
$\displaystyle P(x\ge y\ge z)=6\left(\int_0^w(y-y^2)dy\right)=\frac{1}{2}w^2-\frac{1}{3}w^3.$
(How did we derive the double integral? $\displaystyle \int_0^1\mathbb{1}_{x\ge y}dx=1-y,\,$ then step 2, $\displaystyle \int_0^1(1-y)\mathbb{1}_{y\ge z}dz=y-y^2.)$
Approach 2
We have the cdf of $\min(x,y,z),\,$ $F_{\min}(w)=1-(1-w)^3,\,$ that of $\max(x,y,z),\,$ $F_{\max}(w)=w^3.\,$ The pdf's are as follows: $p_{\min}(w)=3(1-w)^2,\,$ $p_{\max}(w)=3w^2.\,$ The pdf of a uniform variable lying between the two (assuming only 3 draws):
$\displaystyle p_w(w)=3-p_{\min}(w)-p_{\max}(w)=6(w-w^2).$
Why? I don't know exactly, but snaps out immediately.
Approach 3
We option traders are mandated to never accept a theoretical result without the Monte Carlo check, just in case something slipped through the derivations. And, believe me, things slip through derivations.
Solution 4
Consider points lying in a unit cube in the first octant with one corner at the origin. To find the volume of the region of points where the inequality holds, take cross-sections for each value of $z\,$ from $0\,$ to $1.\,$ For any particular value of $z,\,$ the values of $x\,$ and $y\,$ must satisfy $0 \le x \le 1,\,$ $0 \le y \le 1,\,$ $\displaystyle -\frac{2}{3}\le y-x\le\frac{2}{3},\,$ $\displaystyle z-\frac{2}{3}\le x\le z+\frac{2}{3},\,$ $z-\frac{2}{3}\le y\le z+\frac{2}{3}.$
Depending on the value of $z,\,$ the resulting region is a square of area $\displaystyle \frac{4}{9}\,$ (when $z=0\,$ or $1),\,$ or a hexagon of area $\displaystyle \frac{4}{9}+\frac{4(1-z)}{3}\,$ when $\displaystyle \frac{2}{3}\lt z\lt 1).\,$ The region where $\displaystyle z=\frac{1}{6}\,$ is shown.
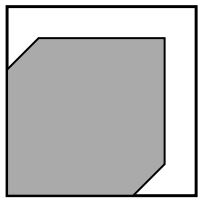
In the cases where $z\,$ is not between $\displaystyle \frac{1}{3}\,$ and $\displaystyle \frac{2}{3},\,$ the area changes linearly with $z\,$ and hence can be averaged to $\displaystyle \frac{1}{2}\left(\frac{4}{9}+\frac{8}{9}\right)=\frac{2}{3}.\,$ This area corresponds to $\displaystyle \frac{2}{3}\,$ of the $z$-values, with the other $\displaystyle \frac{1}{3}\,$ having area $\displaystyle \frac{8}{9},\,$ for a total probability of $\displaystyle \frac{2}{3}\cdot\frac{2}{3}+\frac{1}{3}\cdot\frac{8}{9}=\frac{20}{27}.$
Acknowledgment
This problem #7 from the 2016 American Regional Mathematical League Competition. Solution 1 is by Barry Vanhoff; Solution 2 is by Amit Itagi; Solution 3 is by N. N. Taleb; Proof 4 is the official proof available at the site of the Competition.
N. N. Taleb has generously offered to provide details for his derivation. Gratefully, I took him up at his word. Expanded Solution 3 is the result of that interaction.
Mike Lawler offered an exciting 3d illustration of the relevant region. Mike later used 3d printing to work out the problem with his young sons, see his blog.
Geometric Probability
- Geometric Probabilities
- Are Most Triangles Obtuse?
- Barycentric Coordinates and Geometric Probability
- Bertrand's Paradox
- Birds On a Wire (Problem and Interactive Simulation)
- Buffon's Noodle Simulation
- Averaging Raindrops - an exercise in geometric probability
- Rectangle on a Chessboard: an Introduction
- Marking And Breaking Sticks
- Random Points on a Segment
- Semicircle Coverage
- Hemisphere Coverage
- Overlapping Random Intervals
- Random Intervals with One Dominant
- Points on a Square Grid
- Flat Probabilities on a Sphere
- Probability in Triangle
![]()
|Contact| |Front page| |Contents| |Algebra| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73578670
