Eight Selections in Six Sectors
|
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Probability| |Store|
Copyright © 1996-2012 Alexander Bogomolny
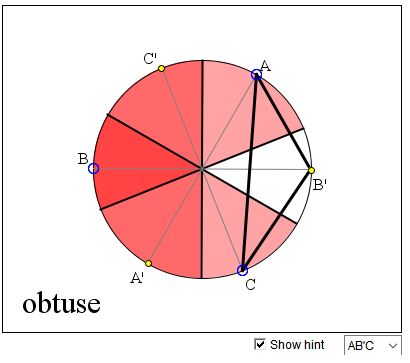
The applet attempts to suggest an argument in favor of the thesis that there are 3 times as many obtuse triangles as there are acute ones.
Three points A, B, C are distributed uniformly on a circle. What is the probability of their forming an obtuse triangle?
| Buy this applet What if applet does not run? |
N. Vasiliev credits V. V. Fok and Yu. V. Chekanov with the following argument.
We shall select a triangle in two steps. First we get three points A, B, C and their antipodes A', B', C' across the center of the circle. Selecting a triangle consists in selecting one of the points in each of three pairs
With each of the six points we associate the semicircle around its antipode. Three points form an obtuse triangle if and only if they lie in a semicircle and this is only if their associated semicircles have a nonempty intersection. The diameters of the associated semicircles form 6 sectors. Each sector serves as an intersection of the associated semicircles for exactly one selection of the vertices, meaning that out of 8 possible selections there are always 6 obtuse (and 2 acute) triangles. The probability that one is obtuse is therefore,
References
Geometric Probability
- Geometric Probabilities
- Are Most Triangles Obtuse?
- Eight Selections in Six Sectors
- Barycentric Coordinates and Geometric Probability
- Bertrand's Paradox
- Birds On a Wire (Problem and Interactive Simulation)
- Buffon's Noodle Simulation
- Averaging Raindrops - an exercise in geometric probability
- Rectangle on a Chessboard: an Introduction
|Activities| |Contact| |Front page| |Contents| |Geometry| |Probability| |Store|
Copyright © 1996-2012 Alexander Bogomolny
| 41143755 |
