Probability in Triangle
What is this about?
Problem
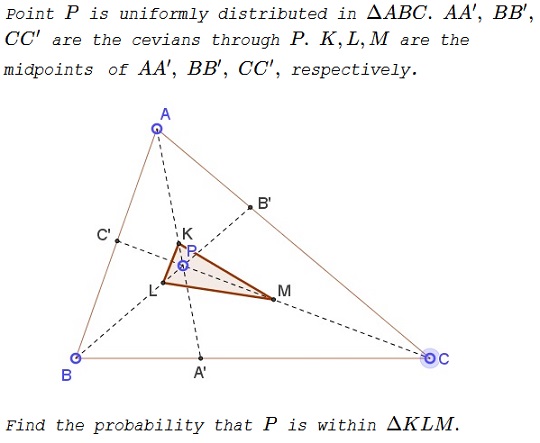
Solution 1
Let $x,y,z$ be the areas of triangles $PBC,$ $PCA,$ and that of $PAB.$ We have
$\displaystyle\begin{align}K&=\frac{(y+z)A+yB+zC}{2(y+z)},\\L&=\frac{xA+(z+x)B+zC}{2(z+x)},\\M&=\frac{xA+yB+(x+y)C}{2(x+y)}.\end{align}$
$P$ is inside $\Delta KLM$ if and only if $P=\alpha K + \beta L +\gamma M,$ with $\alpha,\beta,\gamma\gt 0$ and $\alpha+\beta+\gamma=1,$ i.e.,
$\displaystyle \begin{align} &\frac{\alpha}{2}+\beta\cdot\frac{x}{2(z+x)}+\gamma\cdot\frac{x}{2(x+y)}=\frac{x}{x+y+z}\\ &\alpha\cdot\frac{y}{2(y+z)}+\frac{\beta}{2}+\gamma\cdot\frac{y}{2(x+y)}=\frac{y}{x+y+z}\\ &\alpha\cdot\frac{z}{2(y+z)}+\beta\cdot\frac{z}{2(z+x)}+\frac{\gamma}{2}=\frac{z}{x+y+z}. \end{align}$
Solving that system shows that the signs of $\alpha,\beta,\gamma$ are determined by the signs of $(x+y-z)(x-y+z),$ $(-x+y+z)(x+y-z),$ and $(x-y+z)(-x+y+z),$ respectively.
We shall show that $x+y-z,x-y+z,-x+y+z\gt 0.$ Indeed, assuming to the contrary that, e.g., $x+y-z\le 0$ we get $x-y+z\gt 0$ and $-x+y+z\gt 0$ from which not all $\alpha,\beta,\gamma$ are positive. A contradiction.
we have
$\displaystyle \begin{align} P&=\frac{1}{x+y+z}\cdot (xA+yB+zC)\\ &=\frac{1}{x+y+z}\cdot \small{\left((-x+y+z)\frac{B+C}{2}+(x-y+z)\frac{C+A}{2}+(x+y-z)\frac{A+B}{2}\right)}. \end{align}$
This exactly means that $P$ is interior to $\Delta KLM$ if and only if
$x+y-z\gt 0,~x-y+z\gt 0,~-x+y+z\gt 0.$
In other words $P$ is interior to $\Delta KLM$ iff $P$ is interior to the medial triangle of $\Delta ABC.$ So the probability of $P$ being in $\Delta KLM$ is the same as the probability of its being in the medial triangle, i.e. $\displaystyle \frac{1}{4}.$
Solution 2
If $P=(x:y:z)$ in homogeneous barycentric coordinates, then $A'=(0:y:z),$ and $K=(y+z:y:z).$ From the identity
$\displaystyle \{y+z,y,z\}=(x+y+z)\frac{\{x,y,z\}}{x+y+z}+(-x+y+z)\{1,0,0\},$
we have the ratio
$\displaystyle \frac{PK}{KA}=\frac{-x+y+z}{x+y+z}.$
the equation $-x+y+z=0$ corresponds to the line parallel to $BC$ through the midpoints of $AB$ and $AC.$ The ratio $PK:KA$ is positive if and only if $P$ lies in the half plane determined by this parallel not containing $A.$
Therefore, the point $P$ is interior to $\Delta KLM$ when $P$ is interior to the medial triangle of $\Delta ABC$ and we get that the sought probability is $\displaystyle \frac{1}{4}.$
Acknowledgment
This problem has been inspired by a question from Thanos Kalogerakis. Solution 1 is by Leo Giugiuc, Solution 2 is by Francisco Javier García Capitán
Geometric Probability
- Geometric Probabilities
- Are Most Triangles Obtuse?
- Barycentric Coordinates and Geometric Probability
- Bertrand's Paradox
- Birds On a Wire (Problem and Interactive Simulation)
- Buffon's Noodle Simulation
- Averaging Raindrops - an exercise in geometric probability
- Rectangle on a Chessboard: an Introduction
- Marking And Breaking Sticks
- Random Points on a Segment
- Semicircle Coverage
- Hemisphere Coverage
- Overlapping Random Intervals
- Random Intervals with One Dominant
- Points on a Square Grid
- Flat Probabilities on a Sphere
- Probability in Triangle
![]()
|Contact| |Front page| |Contents| |Algebra| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73568074
