Averaging Raindrops, Part 2
Scott E. Brodie
11/11/2010
We have shown that if x and y are independent random variables ranging uniformly over the interval from 0 to 1 (like the x- and y-coordinates of raindrops which land on the unit square), the average of the minimum of x and y is given by the volume of the pyramid whose base is the unit square, and whose apex is the point (1, 1, 1), which is 1/3:
Can we obtain a similar evaluation for the average of the maximum of x and y?
No problem!
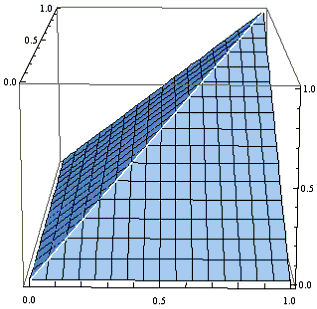
Here is a plot of the function max(x, y) over the unit square:
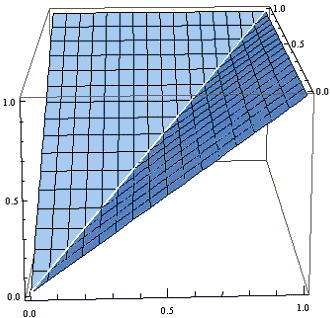
Careful inspection of this surface shows that it is the upper boundary of the union of two pyramids, each congruent to the pyramid in the first figure, but oriented so that its base is one of the vertical faces of the unit cube, and the vertex is at the origin (0, 0, 0). Since we already know that the volume of each of these pyramids is 1/3, the volume of the solid bound by the surface max(x, y) and the sides of the unit cube - and hence the average of max(x, y), since the area of the unit square is 1 - is 2/3.
We may verify our exploration algebraically. Quite obviously
min(x, y) + max(x, y) = x + y.
Using the additivity of the mathematical expectation,
E(x + y) = E(x) + E(y) = 1/2 + 1/2 = 1.
We also get
E(min(x, y) + max(x, y)) = E(min(x, y)) + E(max(x, y)) = 1/3 + 2/3 = 1,
confirming the geometric derivation.
Geometric Probability
|Contact|
|Front page|
|Contents|
|Probability|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
| 
