Are Most Triangles Obtuse?

If one chooses three random points in the plane, what is the probability that they form an obtuse triangle? R. Guy claims, the probability is $3/4$ - at least! However, this is a problem of geometric probabilities and it is reasonable to expect slight complications. As C. Alsina and R. B. Nelsen wrote, this is an old problem, with multiple solutions. One of the earliest solutions appears to be by Lewis Carroll, best known as the author of Alice's Adventures in Wonderland and Through the Looking Glass. Carroll's real name was Charles Lutwidge Dodgson (1832-1898) and he was a lecturer in mathematics at Christ Church, Oxford. In that role he published Pillow Problems Thought Out During Wakeful Hours in 1893. Problem 58 in that collection reads:

Three Points are taken at random on an infinite plane. Find the chance of their being the vertices of an obtuse-angled Triangle.

With a reference to Figure 1 below, Guy remarks that given side $AB$ of $\Delta ABC,$ the positions of the third vertex $C$ for which the triangle is acute are in the shaded region, which constitutes a negligible fraction of the whole plane.

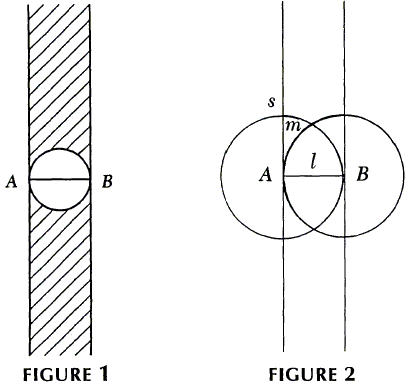
illustration of probbality of a random triangle being obtuse

In Figure 2 the regions are marked, where $C$ makes $AB$ the shortest (s), middle (m), or longest (1) side. Looking at the ratios of the appropriate areas, Carroll finds that when AB is assumed to be the longest side, the probability of $\Delta ABC$ being obtuse is

$\displaystyle\frac{\pi /4}{2\pi /3-\sqrt{3}/2}\approx 0.639.$

In case where AB is the middle side, that probability becomes

$\displaystyle\frac{\pi /2}{\pi /3-\sqrt{3}/2}\approx 0.821.$

Finally, if AB is the shortest side, the probability of $\Delta ABC$ being acute is negligible.

The result of the calculations, as we see and might have expected, depends on the manner in which the calculations have been carried out. The argument is reasonably convincing that there are more obtuse triangles than all others, however it is unclear whether the three cases could be combined into a single answer.

A hundred years after L. Carroll, R. Guy found several elegant approaches to answering the problem. The one I like best begins with an observation that, any triangle possesses the orthocenter which together with the three vertices of the triangle forms an orthocentric system of four points: each point of the four serves as the orthocenter of the triangle formed by the remaining three. Now, for an obtuse triangle the orthocenter lies outside the triangle. It lies inside the triangle only if the triangle is acute. Of the four points in general position (meaning there are no collinearities of three points), only one lies in the interior of the triangle formed by the other three. This is equivalent to saying that any four points (in general position) define 1 acute and 3 obtuse triangles. There are really 3 times as many obtuse triangles as there are acute ones. (This claim could be questioned on the grounds that both quantities are infinite so that their cardinalities do not change when multiplied by 3. Instead, it should be interpreted in terms of probabilities.)

Another observation is that every triangle has a circumcircle. With this in mind, one selects three points on a circle. In this model, the problem has been considered elsewhere. Here, again, the probability was found to be $3/4.$

Remark

There is an extra delightful argument that leads to the same result.

An interesting lecture by Gilbert Strang is available online.

References

C. Alsina, R. B. Nelsen, Charming Proofs, MAA, 2010
R. Guy, There Are Three Times as Many Obtuse-Angled Triangles as There Are Acute-Angled Ones, Mathematics Magazine, Vol. 66, No. 3 (Jun., 1993), pp. 175-179

Geometric Probability

71537168