6th European Mathematical Cup (2017), Junior Problem 4
Problem
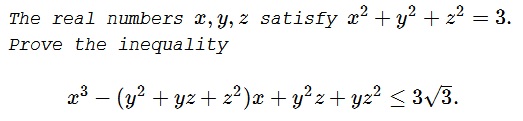
Solution
Observe that, according to Viète's formulas, the polynomial
$\begin{align} f(x)&= x^3 - (y^2 + yz + z^2)x + y^2z+yz^2\\ &=x^3 - [yz-y(y+z)-z(y+z)]x + yz(y + z) \end{align}$
has three real roots: $y,z,-(x+y).$ It follows that $f(x)=(x-y)(x-z)(x+y+z),$ making the required inequality equivalent to
$\displaystyle (x-y)^2(x-z)^2(x+y+z)^2 \le (x^2+y^2+z^2)^3.$
By the AM-GM inequality,
$\displaystyle\begin{align}(x-y)^2(x-z)^2(x+y+z)^2&\le \left(\frac{(x-y)^2+(x-z)^2+(x+y+z)^2}{3}\right)^3\\ &=\left(\frac{3x^2+2y^2+2z^2+2yz}{3}\right)^3, \end{align}$
with equality iff $(x-y)^2=(x-z)^2=(x+y+z)^2.$ Thus suffice it to prove that
$3x^2+2y^2+2z^2+2yz\le3x^2+3y^2+3z^2,$
which is just $(y-z)^2\ge 0,$ with equality for $y=z.$ All the equality conditions hold for $y=z=0$ and $x=\sqrt{3},$ or $y+2x=0,$ i.e., $\displaystyle x=-\frac{1}{\sqrt{3}},$ $\displaystyle y=z=\frac{2}{\sqrt{3}}.$
Acknowledgment
This is Problem 4 (by Miroslav Marinov) from the 2017 European Mathematical Cup (Junior category). I am grateful to Leo Giugiuc for bringing this competition and the problem to my attention and for supplying the beautiful solution above.
- A Cyclic But Not Symmetric Inequality in Four Variables $\left(\displaystyle 5(a+b+c+d)+\frac{26}{abc+bcd+cda+dab}\ge 26.5\right)$
- An Inequality with Constraint $\left((x+1)(y+1)(z+1)\ge 4xyz\right)$
- An Inequality with Constraints II $\left(\displaystyle abc+\frac{2}{ab+bc+ca}\ge\frac{5}{a^2+b^2+c^2}\right)$
- An Inequality with Constraint III $\left(\displaystyle \frac{x^3}{y^2}+\frac{y^3}{z^2}+\frac{z^3}{x^2}\ge 3\right)$
- An Inequality with Constraint IV $\left(\displaystyle\sum_{k=1}^{n}\sqrt{x_k}\ge (n-1)\sum_{k=1}^{n}\frac{1}{\sqrt{x_k}}\right)$
- An Inequality with Constraint VII $\left(|(2x+3y-5z)-3(x+y-5z)|=|-x+10z|\le\sqrt{101}\right)$
- An Inequality with Constraint VIII $\left(\sqrt{24a+1}+\sqrt{24b+1}+\sqrt{24c+1}\ge 15\right)$
- An Inequality with Constraint IX $\left(x^2+y^2\ge x+y\right)$
- An Inequality with Constraint X $\left((x+y+p+q)-(x+y)(p+q)\ge 1\right)$
- Problem 11804 from the AMM $\left(10|x^3 + y^3 + z^3 - 1| \le 9|x^5 + y^5 + z^5 - 1|\right)$
- Sladjan Stankovik's Inequality With Constraint $\left(abc+bcd+cda+dab-abcd\le\displaystyle \frac{27}{16}\right)$
- An Inequality with Constraint XII $\left(abcd\ge ab+bc+cd+da+ac+bd-5\right)$
- An Inequality with Constraint XIV $\left(\small{64(a^2+ab+b^2)(b^2+bc+c^2)(c^2+ca+a^2) \le 3(a+b+c)^6}\right)$
- An Inequality with Constraint XVII $\left(a^3+b^3+c^3\ge 0\right)$
- An Inequality with Constraint in Four Variables II $\left(a^3+b^3+c^3+d^3 + 6abcd \ge 10\right)$
- An Inequality with Constraint in Four Variables III $\left(\displaystyle\small{abcd+\frac{15}{2(ab+ac+ad+bc+bd+cd)}\ge\frac{9}{a^2+b^2+c^2+d^2}}\right)$
- An Inequality with Constraint in Four Variables V $\left(\displaystyle 5\sum \frac{abc}{\sqrt[3]{(1+a^3)(1+b^3)(1+c^3)}}\leq 4\right)$
- An Inequality with Constraint in Four Variables VI $\left(\displaystyle \sum_{cycl}a^2+6\cdot\frac{\displaystyle \sum_{cycl}abc}{\displaystyle \sum_{cycl}a}\ge\frac{5}{3}\sum_{sym}ab\right)$
- A Cyclic Inequality in Three Variables with Constraint $\left(\displaystyle a\sqrt{bc}+b\sqrt{ca}+c\sqrt{ab}+2abc=1\right)$
- Dorin Marghidanu's Cyclic Inequality with Constraint $\left(\displaystyle 2a^2-2\sqrt{2}(b+c)a+3b^2+4c^2-2\sqrt{bc}\gt 0\right)$
- Dan Sitaru's Cyclic Inequality In Three Variables with Constraints $\left(\displaystyle \frac{1}{\sqrt{a+b^2}}+ \frac{1}{\sqrt{b+c^2}}+ \frac{1}{\sqrt{c+a^2}}\ge\frac{1}{\sqrt{a+b+c}}\right)$
- Dan Sitaru's Cyclic Inequality In Three Variables with Constraints II $\left(\displaystyle \sum_{cycl}\frac{\displaystyle \frac{x}{y}+1+\frac{y}{x}}{\displaystyle \frac{1}{x}+\frac{1}{y}}\le 9\right)$
- Dan Sitaru's Cyclic Inequality In Three Variables with Constraints III $\left(\displaystyle 12+\sum_{cycl}\left(\sqrt{\frac{x^3}{y}}+\sqrt{\frac{x^3}{y}}\right)\ge 8(x+y+z)\right)$
- Inequality with Constraint from Dan Sitaru's Math Phenomenon $\left(\displaystyle b+2a+20\ge 2\sum_{cycl}\frac{a^2+ab+b^2}{a+b}\ge b+2c+20\right)$
- Another Problem from the 2016 Danubius Contest $\left(\displaystyle \frac{1}{a^2+2}+\frac{1}{b^2+2}+\frac{1}{c^2+2}\le 1\right)$
- Gireaux's Theorem (If a continuous function of several variables is defined on a hyperbrick and is convex in each of the variables, it attains its maximum at one of the corners)
- An Inequality with a Parameter and a Constraint $\left(\displaystyle a^4+b^4+c^4+\lambda abc\le\frac{\lambda +1}{27}\right)$
- Unsolved Problem from Crux Solved $\left(a_1a_2a_3a_4a_5a_6\le\displaystyle \frac{5}{2}\right)$
- An Inequality With Six Variables and Constraints Find the range of $\left(a^2+b^2+c^2+d^2+e^2+f^2\right)$
- Cubes Constrained $\left(3(a^4+b^4)+2a^4b^4\le 8\right)$
- Dorin Marghidanu's Inequality with Constraint $\left(\displaystyle \frac{1}{a_1+1}+\frac{2}{2a_2+1}+\frac{3}{3a_3+1}\ge 4\right)$
- Dan Sitaru's Integral Inequality with Powers of a Function $\left(\displaystyle\left(\int_0^1f^5(x)dx\right)\left(\int_0^1f^7(x)dx\right)\left(\int_0^1f^9(x)dx\right)\ge 2\right)$
- Michael Rozenberg's Inequality in Three Variables with Constraints $\left(\displaystyle 4\sum_{cycl}ab(a^2+b^2)\ge\sum_{cycl}a^4+5\sum_{cycl}a^2b^2+2abc\sum_{cycl}a\right)$
- Dan Sitaru's Cyclic Inequality In Three Variables with Constraints IV $\left(\displaystyle \frac{(4x^2y^2+1)(36y^2z^2+1)(9x^2z^2+1)}{2304x^2y^2z^2}\geq \frac{1}{(x+2y+3z)^2}\right)$
- Refinement on Dan Sitaru's Cyclic Inequality In Three Variables $\left(\displaystyle \frac{(4x^2y^2+1)(36y^2z^2+1)(9x^2z^2+1)}{2304x^2y^2z^2}\geq \frac{1}{3\sqrt{3}}\right)$
- An Inequality with Arbitrary Roots $\left(\displaystyle \sum_{cycl}\left(\sqrt[n]{a+\sqrt[n]{a}}+\sqrt[n]{a-\sqrt[n]{a}}\right)\lt 18\right)$
- Leo Giugiuc's Inequality with Constraint $\left(\displaystyle 2\left(\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}\right)\le ab+bc+ca\right)$
- Problem From the 2016 IMO Shortlist $\left(\displaystyle \sqrt[3]{(a^2+1)(b^2+1)(c^2+1)}\le\left(\frac{a+b+c}{3}\right)^2+1\right)$
- Dan Sitaru's Cyclic Inequality with a Constraint and Cube Roots $\left(\displaystyle \sum_{cycl}\sqrt[3]{\frac{abc}{(a+1)(b+1)(c+1)}}\le\frac{4}{5}\right)$
- Dan Sitaru's Cyclic Inequality with a Constraint and Cube Roots II $\left(\displaystyle \sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}+\sqrt[3]{d}\le\sqrt[3]{abcd}\right)$
- A Simplified Version of Leo Giugiuc's Inequality from the AMM $\left(\displaystyle a^3+b^3+c^3\ge 3\right)$
- Kunihiko Chikaya's Inequality $\displaystyle \small{\left(\frac{(a^{10}-b^{10})(b^{10}-c^{10})(c^{10}-a^{10})}{(a^{9}+b^{9})(b^{9}+c^{9})(c^{9}+a^{9})}\ge\frac{125}{3}[(a-b)^3+(b-c)^3+(c-a)^3]\right)}$
- A Cyclic Inequality on [-1,1] $\left(xy+yz+zx\ge 1\right)$
- An Inequality with Two Triples of Variables $\left(\displaystyle\sum_{cycl}ux\ge\sqrt{\left(\sum_{cycl}xy\right)\left(2\sum_{cycl}uv-\sum_{cycl}u^2\right)}\right)$
- 6th European Mathematical Cup (2017), Junior Problem 4 $\left(x^3 - (y^2 + yz + z^2)x + y^2z + yz^2 \le 3\sqrt{3}\right)$
- Dorin Marghidanu's Example $\left(\displaystyle\frac{\displaystyle\frac{1}{b_1}+\frac{2}{b_2}+\frac{3}{b_3}}{1+2+3}\ge\frac{1+2+3}{b_1+2b_2+3b_3}\right)$
- A Trigonometric Inequality with Ordered Triple of Variables $\left((x+y)\sin x+(x-z)\sin y\lt (y+z)\sin x\right)$
- Three Variables, Three Constraints, Two Inequalities (Only One to Prove) - by Leo Giugiuc $\bigg(a+b+c=0$ and $a^2+b^2+c^2\ge 2$ Prove that $abc\ge 0\bigg)$
- Hung Nguyen Viet's Inequality with a Constraint $\left(1+2(xy+yz+zx)^2\ge (x^3+y^3+z^3+6xyz)^2\right)$
- A Cyclic Inequality by Seyran Ibrahimov $\left(\displaystyle \sum_{cycl}\frac{x}{y^4+y^2z^2+z^4}\le\frac{1}{(xyz)^2}\right)$
- Dan Sitaru's Cyclic Inequality In Three Variables with Constraints V $\left(\displaystyle \frac{1}{\sqrt{ab(a+b)}}+\frac{1}{\sqrt{bc(b+c)}}+\frac{1}{\sqrt{ca(c+a)}}\le 3+\frac{a+b+c}{abc}\right)$
- Cyclic Inequality In Three Variables From Kvant $\left(\displaystyle \frac{a}{bc+1}+\frac{b}{ca+1}+\frac{c}{ab+1}\le 2\right)$
- Cyclic Inequality In Three Variables From Vietnam by Rearrangement $\left(\displaystyle \frac{x^3+y^3}{y^2+z^2}+\frac{y^3+z^3}{z^2+x^2}+\frac{z^3+x^3}{x^2+y^2}\le 3\right)$
- A Few Variants of a Popular Inequality And a Generalization $\left(\displaystyle \frac{1}{(a+b)^2+4}+\frac{1}{(b+c)^2+4}+\frac{1}{(c+a)^2+4}\le \frac{3}{8}\right)$
- Two Constraints, One Inequality by Qing Song $\left(|a|+|b|+|c|\ge 6\right)$
- A Moscow Olympiad Question with Two Inequalities $\left(\displaystyle b^2\gt 4ac\right)$ A Problem form the Short List of the 2018 JBMO $\left(ab^3+bc^3+cd^3+da^3\ge a^2b^2+b^2c^2+c^2d^2+d^2a^2\right)$
- An Inequality from a Mongolian Exam $\left(\displaystyle 2\sum_{i=1}^{2n-1}(x_i-A)^2\ge \sum_{i=1}^{2n-1}(x_i-x_n)^2\right)$
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73573830
