Dan Sitaru's Cyclic Inequality with a Constraint and Cube Roots II
Problem
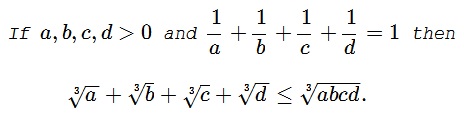
Solution 1
By the AM-GM inequality,
$\displaystyle \begin{align} 1&=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}=\frac{1}{3}\sum_{cycl}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\\ &\ge \frac{1}{3}\cdot 3\cdot\sum_{cycl}\frac{1}{\sqrt[3]{abc}}=\sum_{cycl}\frac{1}{\sqrt[3]{abc}}. \end{align}$
Thus,$\displaystyle \sum_{cycl}\frac{1}{\sqrt[3]{abc}}\le 1.$ Multiplying this by $\sqrt[3]{abcd}$ yields the required inequality.
Equality is attained for $a=b=c=d=4.$
Solution 2
Due to the constraint,
$\displaystyle 1=\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}\right)^3\ge 4^2\left(\frac{1}{abc}+\frac{1}{bcd}+\frac{1}{cda}+\frac{1}{dab}\right),$
implying
$\displaystyle \frac{1}{abc}+\frac{1}{bcd}+\frac{1}{cda}+\frac{1}{dab}\le\frac{1}{4^2}.$
Hence, $\displaystyle 4^2(a+b+c+d)\le abcd,\,$ so that $\displaystyle \sqrt[3]{4^2(a+b+c+d)}\le \sqrt[3]{abcd},$ but (due to concavity of $y=\sqrt[3]{x},$ for $x\ge 0,$ and Jensen's inequality) $\displaystyle \sum_{cycl}\sqrt[3]{a}\le\sqrt[3]{4^2\sum_{cycl}a},$ such that, finally, $\displaystyle \sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}+\sqrt[3]{d}\le\sqrt[3]{abcd}.$
Solution 3
Let $\displaystyle \frac{1}{a}=p^3,~\frac{1}{b}=q^3,~\frac{1}{c}=r^3,~\frac{1}{d}=s^3.$ From Muirhead (or four AM-GM's taking three cubes at a time),
$\displaystyle pqr+qrs+rsp+spq\leq p^3+q^3+r^3+s^3=1$.
Dividing both sides by $pqrs$, we get
$\displaystyle \frac{1}{p}+\frac{1}{q}+\frac{1}{r}+\frac{1}{s}\leq \frac{1}{pqrs},$
which in terms of $a-d$ is the inequality to be proved.
Solution 4
We have the Harmonic Mean $\displaystyle \frac{\displaystyle 4}{\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}}=4$, so by the AM-HM inequality, $a+b+c+d \geq 16.$ Also, by the AM-GM inequality,
$\displaystyle 1=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}\geq 4 \sqrt[4]{\frac{1}{a b c d}}.$
Therefore, $\displaystyle \sqrt[3]{a b c d}\geq 4\times 2^{2/3}.$ So,we have (by the Power-Mean inequality)
$\displaystyle \frac{1}{64} \left(\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}+\sqrt[3]{d}\right)^3\leq \frac{1}{4} (a+b+c+d)\leq 4.$
Finally
$\displaystyle \sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}+\sqrt[3]{d}\leq 4\times 2^{2/3}\le\sqrt[3]{a b c d}.$
Acknowledgment
Dan Sitaru has kindly posted the problem at the CutTheKnotMath facebook page, with solutions by Yadamsuren Myagmarsuren (Solution 1) and Sanong Hauerai (Solution 2). The problem was originally publshed at the Romanian Mathematical Magazine. Solution 3 is by Amit Itagi; Solution 4 is by N. N. Taleb.
- A Cyclic But Not Symmetric Inequality in Four Variables $\left(\displaystyle 5(a+b+c+d)+\frac{26}{abc+bcd+cda+dab}\ge 26.5\right)$
- An Inequality with Constraint $\left((x+1)(y+1)(z+1)\ge 4xyz\right)$
- An Inequality with Constraints II $\left(\displaystyle abc+\frac{2}{ab+bc+ca}\ge\frac{5}{a^2+b^2+c^2}\right)$
- An Inequality with Constraint III $\left(\displaystyle \frac{x^3}{y^2}+\frac{y^3}{z^2}+\frac{z^3}{x^2}\ge 3\right)$
- An Inequality with Constraint IV $\left(\displaystyle\sum_{k=1}^{n}\sqrt{x_k}\ge (n-1)\sum_{k=1}^{n}\frac{1}{\sqrt{x_k}}\right)$
- An Inequality with Constraint VII $\left(|(2x+3y-5z)-3(x+y-5z)|=|-x+10z|\le\sqrt{101}\right)$
- An Inequality with Constraint VIII $\left(\sqrt{24a+1}+\sqrt{24b+1}+\sqrt{24c+1}\ge 15\right)$
- An Inequality with Constraint IX $\left(x^2+y^2\ge x+y\right)$
- An Inequality with Constraint X $\left((x+y+p+q)-(x+y)(p+q)\ge 1\right)$
- Problem 11804 from the AMM $\left(10|x^3 + y^3 + z^3 - 1| \le 9|x^5 + y^5 + z^5 - 1|\right)$
- Sladjan Stankovik's Inequality With Constraint $\left(abc+bcd+cda+dab-abcd\le\displaystyle \frac{27}{16}\right)$
- An Inequality with Constraint XII $\left(abcd\ge ab+bc+cd+da+ac+bd-5\right)$
- An Inequality with Constraint XIV $\left(\small{64(a^2+ab+b^2)(b^2+bc+c^2)(c^2+ca+a^2) \le 3(a+b+c)^6}\right)$
- An Inequality with Constraint XVII $\left(a^3+b^3+c^3\ge 0\right)$
- An Inequality with Constraint in Four Variables II $\left(a^3+b^3+c^3+d^3 + 6abcd \ge 10\right)$
- An Inequality with Constraint in Four Variables III $\left(\displaystyle\small{abcd+\frac{15}{2(ab+ac+ad+bc+bd+cd)}\ge\frac{9}{a^2+b^2+c^2+d^2}}\right)$
- An Inequality with Constraint in Four Variables V $\left(\displaystyle 5\sum \frac{abc}{\sqrt[3]{(1+a^3)(1+b^3)(1+c^3)}}\leq 4\right)$
- An Inequality with Constraint in Four Variables VI $\left(\displaystyle \sum_{cycl}a^2+6\cdot\frac{\displaystyle \sum_{cycl}abc}{\displaystyle \sum_{cycl}a}\ge\frac{5}{3}\sum_{sym}ab\right)$
- A Cyclic Inequality in Three Variables with Constraint $\left(\displaystyle a\sqrt{bc}+b\sqrt{ca}+c\sqrt{ab}+2abc=1\right)$
- Dorin Marghidanu's Cyclic Inequality with Constraint $\left(\displaystyle 2a^2-2\sqrt{2}(b+c)a+3b^2+4c^2-2\sqrt{bc}\gt 0\right)$
- Dan Sitaru's Cyclic Inequality In Three Variables with Constraints $\left(\displaystyle \frac{1}{\sqrt{a+b^2}}+ \frac{1}{\sqrt{b+c^2}}+ \frac{1}{\sqrt{c+a^2}}\ge\frac{1}{\sqrt{a+b+c}}\right)$
- Dan Sitaru's Cyclic Inequality In Three Variables with Constraints II $\left(\displaystyle \sum_{cycl}\frac{\displaystyle \frac{x}{y}+1+\frac{y}{x}}{\displaystyle \frac{1}{x}+\frac{1}{y}}\le 9\right)$
- Dan Sitaru's Cyclic Inequality In Three Variables with Constraints III $\left(\displaystyle 12+\sum_{cycl}\left(\sqrt{\frac{x^3}{y}}+\sqrt{\frac{x^3}{y}}\right)\ge 8(x+y+z)\right)$
- Inequality with Constraint from Dan Sitaru's Math Phenomenon $\left(\displaystyle b+2a+20\ge 2\sum_{cycl}\frac{a^2+ab+b^2}{a+b}\ge b+2c+20\right)$
- Another Problem from the 2016 Danubius Contest $\left(\displaystyle \frac{1}{a^2+2}+\frac{1}{b^2+2}+\frac{1}{c^2+2}\le 1\right)$
- Gireaux's Theorem (If a continuous function of several variables is defined on a hyperbrick and is convex in each of the variables, it attains its maximum at one of the corners)
- An Inequality with a Parameter and a Constraint $\left(\displaystyle a^4+b^4+c^4+\lambda abc\le\frac{\lambda +1}{27}\right)$
- Unsolved Problem from Crux Solved $\left(a_1a_2a_3a_4a_5a_6\le\displaystyle \frac{5}{2}\right)$
- An Inequality With Six Variables and Constraints Find the range of $\left(a^2+b^2+c^2+d^2+e^2+f^2\right)$
- Cubes Constrained $\left(3(a^4+b^4)+2a^4b^4\le 8\right)$
- Dorin Marghidanu's Inequality with Constraint $\left(\displaystyle \frac{1}{a_1+1}+\frac{2}{2a_2+1}+\frac{3}{3a_3+1}\ge 4\right)$
- Dan Sitaru's Integral Inequality with Powers of a Function $\left(\displaystyle\left(\int_0^1f^5(x)dx\right)\left(\int_0^1f^7(x)dx\right)\left(\int_0^1f^9(x)dx\right)\ge 2\right)$
- Michael Rozenberg's Inequality in Three Variables with Constraints $\left(\displaystyle 4\sum_{cycl}ab(a^2+b^2)\ge\sum_{cycl}a^4+5\sum_{cycl}a^2b^2+2abc\sum_{cycl}a\right)$
- Dan Sitaru's Cyclic Inequality In Three Variables with Constraints IV $\left(\displaystyle \frac{(4x^2y^2+1)(36y^2z^2+1)(9x^2z^2+1)}{2304x^2y^2z^2}\geq \frac{1}{(x+2y+3z)^2}\right)$
- Refinement on Dan Sitaru's Cyclic Inequality In Three Variables $\left(\displaystyle \frac{(4x^2y^2+1)(36y^2z^2+1)(9x^2z^2+1)}{2304x^2y^2z^2}\geq \frac{1}{3\sqrt{3}}\right)$
- An Inequality with Arbitrary Roots $\left(\displaystyle \sum_{cycl}\left(\sqrt[n]{a+\sqrt[n]{a}}+\sqrt[n]{a-\sqrt[n]{a}}\right)\lt 18\right)$
- Leo Giugiuc's Inequality with Constraint $\left(\displaystyle 2\left(\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}\right)\le ab+bc+ca\right)$
- Problem From the 2016 IMO Shortlist $\left(\displaystyle \sqrt[3]{(a^2+1)(b^2+1)(c^2+1)}\le\left(\frac{a+b+c}{3}\right)^2+1\right)$
- Dan Sitaru's Cyclic Inequality with a Constraint and Cube Roots $\left(\displaystyle \sum_{cycl}\sqrt[3]{\frac{abc}{(a+1)(b+1)(c+1)}}\le\frac{4}{5}\right)$
- Dan Sitaru's Cyclic Inequality with a Constraint and Cube Roots II
- A Simplified Version of Leo Giugiuc's Inequality from the AMM $\left(\displaystyle a^3+b^3+c^3\ge 3\right)$
- Kunihiko Chikaya's Inequality $\displaystyle \small{\left(\frac{(a^{10}-b^{10})(b^{10}-c^{10})(c^{10}-a^{10})}{(a^{9}+b^{9})(b^{9}+c^{9})(c^{9}+a^{9})}\ge\frac{125}{3}[(a-b)^3+(b-c)^3+(c-a)^3]\right)}$
- A Cyclic Inequality on [-1,1] $\left(xy+yz+zx\ge 1\right)$
- An Inequality with Two Triples of Variables $\left(\displaystyle\sum_{cycl}ux\ge\sqrt{\left(\sum_{cycl}xy\right)\left(2\sum_{cycl}uv-\sum_{cycl}u^2\right)}\right)$
- 6th European Mathematical Cup (2017), Junior Problem 4 $\left(x^3 - (y^2 + yz + z^2)x + y^2z + yz^2 \le 3\sqrt{3}\right)$
- Dorin Marghidanu's Example $\left(\displaystyle\frac{\displaystyle\frac{1}{b_1}+\frac{2}{b_2}+\frac{3}{b_3}}{1+2+3}\ge\frac{1+2+3}{b_1+2b_2+3b_3}\right)$
- A Trigonometric Inequality with Ordered Triple of Variables $\left((x+y)\sin x+(x-z)\sin y\lt (y+z)\sin x\right)$
- Three Variables, Three Constraints, Two Inequalities (Only One to Prove) - by Leo Giugiuc $\bigg(a+b+c=0$ and $a^2+b^2+c^2\ge 2$ Prove that $abc\ge 0\bigg)$
- Hung Nguyen Viet's Inequality with a Constraint $\left(1+2(xy+yz+zx)^2\ge (x^3+y^3+z^3+6xyz)^2\right)$
- A Cyclic Inequality by Seyran Ibrahimov $\left(\displaystyle \sum_{cycl}\frac{x}{y^4+y^2z^2+z^4}\le\frac{1}{(xyz)^2}\right)$
- Dan Sitaru's Cyclic Inequality In Three Variables with Constraints V $\left(\displaystyle \frac{1}{\sqrt{ab(a+b)}}+\frac{1}{\sqrt{bc(b+c)}}+\frac{1}{\sqrt{ca(c+a)}}\le 3+\frac{a+b+c}{abc}\right)$
- Cyclic Inequality In Three Variables From Kvant $\left(\displaystyle \frac{a}{bc+1}+\frac{b}{ca+1}+\frac{c}{ab+1}\le 2\right)$
- Cyclic Inequality In Three Variables From Vietnam by Rearrangement $\left(\displaystyle \frac{x^3+y^3}{y^2+z^2}+\frac{y^3+z^3}{z^2+x^2}+\frac{z^3+x^3}{x^2+y^2}\le 3\right)$
- A Few Variants of a Popular Inequality And a Generalization $\left(\displaystyle \frac{1}{(a+b)^2+4}+\frac{1}{(b+c)^2+4}+\frac{1}{(c+a)^2+4}\le \frac{3}{8}\right)$
- Two Constraints, One Inequality by Qing Song $\left(|a|+|b|+|c|\ge 6\right)$
- A Moscow Olympiad Question with Two Inequalities $\left(\displaystyle b^2\gt 4ac\right)$ A Problem form the Short List of the 2018 JBMO $\left(ab^3+bc^3+cd^3+da^3\ge a^2b^2+b^2c^2+c^2d^2+d^2a^2\right)$
- An Inequality from a Mongolian Exam $\left(\displaystyle 2\sum_{i=1}^{2n-1}(x_i-A)^2\ge \sum_{i=1}^{2n-1}(x_i-x_n)^2\right)$
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73580076
