|
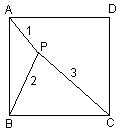
Inside a square ABCD, a point P is selected such that AP = 1, BP = 2, CP = 3. Find ∠APB.
|
The following solution is by Murray Klamkin.
Rotate the square through 90° around point B. Let P' be the image of P, A' that of A, and D' of D. Connect P and P'. In ΔBPP', BP = BP' and ∠P'BP is right. The triangle is also isosceles so that ∠BPP' = 45°. From the Pythagorean Theorem, PP'2 = 8.
In ΔAPP', PP'2 + AP2 = AP'2 (8 + 1 = 9). Therefore, by the converse of the Pythagorean Theorem, the triangle is right and ∠P'PA = 90°.
Summing up, ∠APB = ∠BPP' + ∠P'PA = 45° + 90° = 135°.
A similar approach works for a similar problem where point P is at distances 3, 4, 5 to the vertices of an equilateral triangle.
Reference
- R. Honsberger, More Mathematical Morsels, MAA, 1991, pp. 4-5.
|Contact|
|Front page|
|Contents|
|Geometry|
|Up|
|Store|
Copyright © 1996-2015 Alexander Bogomolny
|
