Dominoes on a Chessboard
Covering a chessboard with L-shaped and straight trominoes posed two different but very engaging problems. Using larger polyominoes naturally leads to a variety of problems. Perhaps unexpectedly, even the simplest of them - dominos - still afford genuine mathematical entertainment.
A domino is a 2×1 polyomino piece, i.e., a piece that consists of two adjoined squares. Obviously, any rectangular N×M chessboard can be covered with dominoes iff at least one of N and M is even. If both are odd, an empty square can be chosen arbitrarily on the board. The proof is similar to a construction used to solve another problem. So, what else the dominoes are good for? Here's one example.
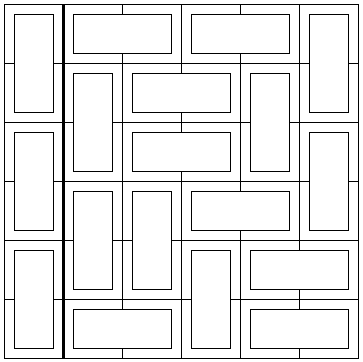
The squares on an N×M chessboard, its pattern, is created by two families of evenly spaced parallel lines: (N-1) horizontal lines and (M-1) vertical lines. A domino piece that covers exactly two squares crosses one such line. Assuming the whole board is covered with dominoes, some of the lines will be crossed, but others may not be. Lets call the lines that have not be crossed fault lines. Prove that every covering of a 6×6 board with dominoes leaves at least one fault line. Give an example of a covering with exactly 1 fault.
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
An important observation is that a chessboard line on a 6×6 board can't be crossed by exactly 1 domino. For, such a line would then split the board into two parts of dimensions 6×t and 6×(6-t), each with an even number of squares of which one square is occupied with a half-domino at hand. If the line is not crossed by another domino, then each of the parts is left with an odd number of squares fully covered with dominoes. A contradiction.
Thus it takes at least two dominoes to cross a line. On a 6×6 board there are 10 lines. It takes
In general, an N×M board can be covered fault-free iff the following condition hold:
N·M is even,
N > 4 and M > 4,
(N, M)
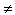(6, 6)!.
References
- A. Engel, Problem-Solving Strategies, Springer Verlag, 1998, p. 35
- S. Golomb, Polyominoes, Princeton University Press; 2nd edition (March 18, 1996)
- A. Soifer, Geometric Etudes in Combinatorial Mathematics, Springer, 2010 (2nd, expanded edition)
- C. W. Trigg, Mathematical Quickies, Dover, 1985, #258
|Activities| |Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2005 Alexander Bogomolny
72088793