Tiling a 12x12 Square with Straight Trominoes
Consider a \(12\times 12\) chessboard (consisting of \(144\) \(1\times 1\) squares.) If one removes 3 corners, can the remainder be covered by \(47\) \(1\times 3\) tiles (straight trominoes.)
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnySolution
Consider a \(12\times 12\) chessboard (consisting of \(144\) \(1\times 1\) squares.) If one removes 3 corners, can the remainder be covered by \(47\) \(1\times 3\) tiles (straight trominoes.)

The answer to the question is negative. To see that, position the board as shown below, with the only remaining corner in the lower left. Color the board in three colors:
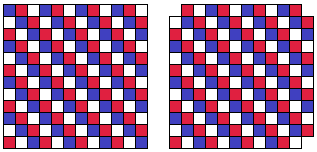
Now, the rows 2-11 contain each exactly 40 squares of each of the colors. What is important is the number of squares of the three colors in the top and bottom rows. There are 8 red, 6 blue, and 7 white squares. However, every tromino - however placed on the board - covers exactly one square of each color. Thus it is impossible to cover the mutilated board with straight trominoes.
References
- M. I. Krusemeyer, G. T. Gilbert, L. C. Larson, A Mathematical Orchard, MAA, 2012, #33
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581323
