Tiling Rectangles with L-Trominoes
L-tromino is a shape consisting of three equal squares joined at the edges to form a shape resembling the capital letter L. There is a fundamental result of covering an N×N square with L-trominos and a single monomino. Here we are concerned with a different question: what kind of rectangles can be completely tiled with L-trominos?
The applet below helps you experiment with the problem. It takes three clicks to place an L-tromino on the board. Click on yet uncovered square and move (not drag) the cursor to an availble neighbor. Click and move the cursor to complete an L-shape at another available square.
| What if applet does not run? |
|Contact| |Front page| |Contents| |Games|
Copyright © 1996-2018 Alexander BogomolnyThe following two observations must be obvious:
First of all, since an L-tromino consists of 3 squares, a rectangle tiled by a number of L-trominoes must consist of a multiple of 3 squares. So, for example, a 4×5 rectangle could not be tiled by L-trominoes. This means that, for a rectangle to be tiled with L-trominoes, one of its sides must be divisible by 3. This is a necessary but not a sufficient condition. Indeed, rectangles 1×3, 3×3 and 5×3 could not be so tiled, as can be easily seen with the help of the applet.
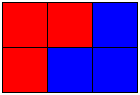
Secondly, the 2×3 is the smallest rectangle that could be tiled by L-trominoes:
Alexander Soifer splits the proof of the main result concerning the general case of the tiling with L-trominoes, into a sequence of exercises:
Exercise 2.2 Find the smallest square that can be tiled with L-trominoes.
Exercise 2.3 Find all integers b such that a 2×b rectangle can be tiled using L-trominoes.
Exercise 2.4 Find all integers b such that a 3×b rectangle can be tiled using L-trominoes.
Combining the two last exercises we obtain the following
Theorem 2.1
Let a, b be the integers such that 2 ≤ a ≤ 3 and a ≤ b. An a×b rectangle can be tiled by L-trominoes if and only if ab is divisible by 6.
(This is equivalent to saying that, with 2 ≤ a ≤ 3 and a ≤ b, one of the numbers a, b is divisible by 2 and the other by 3.)
The next sequence of exercises applies to the case where 4 ≤ a ≤ b.
Exercise 2.5 Prove that a 5×6 rectangle can be tiled using L-trominoes.
Exercise 2.6 Prove that a 5×9 rectangle can be tiled using L-trominoes.
Exercise 2.7 Prove that a 9×9 rectangle can be tiled using L-trominoes.
Exercise 2.8 Prove that that if b > 5 and b is divisible by 3 then a 5×b rectangle can be tiled using L-trominoes.
Exercise 2.9 Prove that that if b is divisible by 3 and an a×b rectangle can be tiled L-trominoes, then this is also true for an
Exercise 2.10 Let the integers a, b satisfy the conditions
Theorem 2.2
An a×b rectangle where a ≥ 4, b ≥ 4 can be tiled with L-trominoes if and only if ab is divisible by 3.
Combining the statements of Theorems 2.1 and 2.2 gives
Theorem 2.3
Let a, b be the integers such that 2 ≤ a ≤ b. An a×b rectangle can be tiled with L-trominoes if and only if one of the following conditions holds:
- a = 3 and b is even;
- a ≠ 3 and ab is divisible by 3.
Reference
- S. Golomb, Polyominoes, Princeton University Press; 2nd edition (March 18, 1996)
- A. Soifer, Geometric Etudes in Combinatorial Mathematics, Springer, 2010 (2nd, expanded edition), pp 7-9
|Contact| |Front page| |Contents| |Games|
Copyright © 1996-2018 Alexander Bogomolny73559654
