Tromino Puzzle: Deficient Squares
S. Golomb gave an inductive proof to the following fact: any 2n×2n board with one square removed can be tiled by right (or L-) trominoes - a piece formed by three adjacent squares in the shape of an L. Golomb's proof of the theorem became a model of elegance in elementary mathematics.
I-Ping Chu and Richard Johnsonbaugh extended Golomb's result to squares with sides not necessarily a power of 2. More accurately:
Theorem
If n ≠ 5, then a deficient n×n board can be tiled with L-trominoes if and only if n is not a multiple of 3.
(The board is deficient if one of the small unit squares is missing.)
Some 5×5 deficient boards can be tiled, others cannot. Although 5 appears as an exceptional case in the theorem, the 5×5 board with a removed corner can be tiled and plays an important role in the proof. The proof does exploits other special cases.
The applet below helps you test your understanding of the theorem by tiling the board manually. It takes three clicks to place a tromino piece on the board: click on three adjacent squares in sequence. (Do not drag the mouse.)
| What if applet does not run? |
Note that for small (2×2 and 4×4) boards the solution is unique and follows Golomb's proof. For larger boards, viz. starting with 8×8, this is no longer true: there is a good deal of solutions. However, some thinking is still required to tile the board and, more often than not, careless tiling will produce 1 and 2 squares pockets.
Another applet provides additional insight into the tiling with L-trominoes.
Interstingly, we run into an entirely different situation if we try to cover the chessboard with straight trominos. Now, we'll have to consider very carefully which single square may or may not be removed!
References
- I-Ping Chu, Richard Johnsonbaugh, Tiling Deficient Boards with Trominoes, Mathematics Magazine, Vol. 59, No. 1 (Feb., 1986), pp. 34-40
|Contact| |Front page| |Contents| |Games|
Copyright © 1996-2018 Alexander BogomolnyTheorem
If n ≠ 5, then a deficient n×n board can be tiled with L-trominoes if and only if n is not a multiple of 3.
The proof is a consequences of several partial results.
Proposition 1
A 5×5 board with one corner square removed can be tiled
The proof is by inspection:
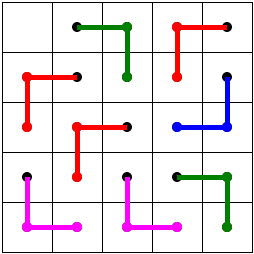
Observe that the board with any of the squares next to a corner one removed could not be tiled with L-trominoes.
Proposition 2
A (2i)×(3j) board, i, j > 1, can be tiled.
Such a board could be tiled by 2×3 rectangles each composed of 2 trominoes:
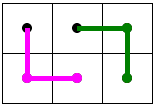
More general rectangles can be tiled with L-trominoes, but the above is the only case used below.
Proposition 3
Every deficient 7×7 board can be tiled.
The proof is again by inspection. There are just a few cases to consider. Enumerate squares starting in the upper left corner of the board with two integers
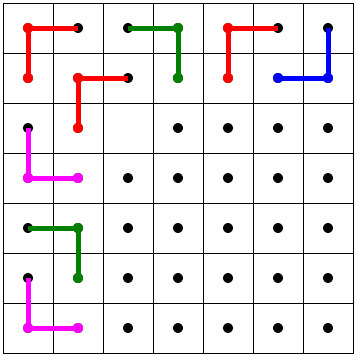
The untiled portion of the board is the deficient 5×5 board from Proposition 1 and can be tiled. If we enumerate squares starting in the upper left corner of the board with two integers (row, column), the diagram tells us that the 7×7 board with the
This diagram serves to show tilings with one of the squares - (1, 1), (1, 2), (2, 2), (2, 1) - removed.
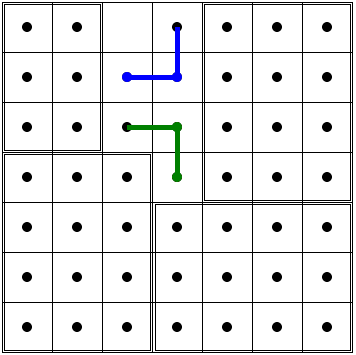
This diagram serves to show tilings with one of squares - (1, 3), (2, 3), (1, 4), (2, 4) - removed.
Two additional tilings (without (4, 4) and (3, 4) squares) complete the proof:
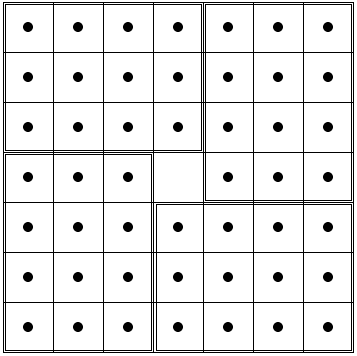
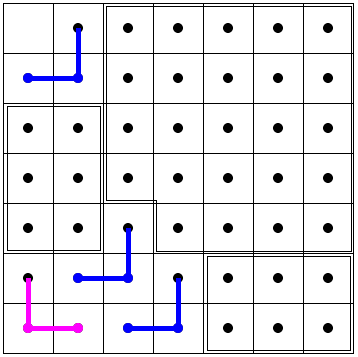
Proposition 4
Any deficient n×n board, with n is odd, n > 5, and not divisible by 3, can be tiled by L-trominoes.
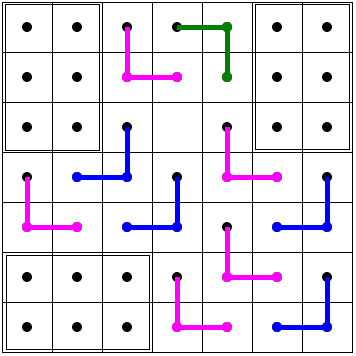
First, we examine a deficient 11×11 board. As the diagram suggests, the board can be split into the a
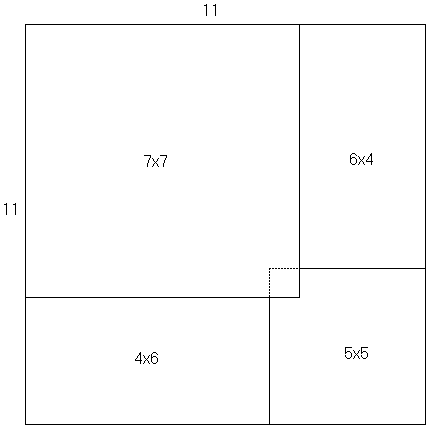
As it was already shown, all four can be tiled with L-trominoes.
From here we proceed by induction. Assume that n is odd, not divisible by 3, and greater than 11. For the inductive step, assume that the statement holds for all smaller odd n not divisible by 3.
Split the board as shown below. The (n - 6)×(n - 6) pieces is assumed to contain the missing square.

If n is odd and not divisible by 3, so is (n - 6), making the
Proposition 5
Any deficient n×n board, with n even, greater than 1 and not divisible by 3 can be tiled with L-trominoes.
We start the induction with the observation that the 2×2, 4×4, and 8×8 deficient boards can be tiled (either by inspection or from Golomb's theorem).
Assume n is even, greater than 8, and is not divisible by 3. Suppose also that all smaller boards with such n can be tiled. Split the board into 4 pieces as shown:
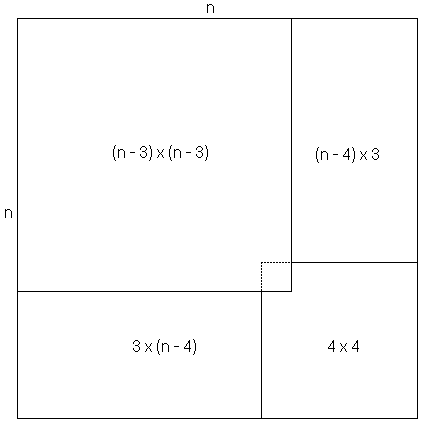
We assume that the missing square is located in the
A combination of the 5 propositions proves the theorem:
If n ≠ 5, then a deficient n×n board can be tiled with L-trominoes if and only if n is not a multiple of 3.
|Contact| |Front page| |Contents| |Games|
Copyright © 1996-2018 Alexander Bogomolny73580377
