Covering A Chessboard With Domino
One of the problems we looked into when discussing the Pigeonhole Principle had to do with covering a mangled chessboard with pieces of domino:
Consider a chessboard with two of the diagonally opposite corners removed. Is it possible to cover the board with pieces of domino whose size is exactly two board squares?
One would expect that if the removed squares were of different colors both the answer and solution would be quite different. Indeed, cover the whole chessboard with pieces of domino. Cut two squares from under one of the pieces. The remaining portion of the board will still be covered with the remaining pieces of domino. Thus, at least, sometimes the remaining board is "coverable." As a warm-up problem you may consider this one:
Problem 1
Cover two arbitrary but adjacent squares of a chessboard with a piece of domino. Is it always possible to cover the remaining portion of the board with domino without disturbing the original piece?
Now, you may want to go further and relax one of the conditions in Problem 1: what if the squares are not adjacent? We already have a solution if they have the same color. There remains then just one case.
Problem 2
Two arbitrary squares of different colors have been removed from a chessboard. Is it possible to cover the remaining portion of the board with domino so that each domino piece covers exactly two squares?
Solution
Yes, it's always possible. To see this, draw two forks as on the diagram. This splits the chessboard into a chain of alternating squares. It takes only a little experimentation to convince oneself that the chain can be traversed by starting at any square and covering two squares at a time with a piece of domino. This observation actually solves the problem.
Note: This theorem and the proof are due to Ralph Gomory. Splitting of a chessboard into a chain of alternating squares is far from unique. For example, mazes associated with plane filling curves - Hilbert's or Peano's - will do the job.
What would be the next question to ask related to covering of a chessboard with domino? My son David came up with the following question:
Problem 3
Assume at every step we remove a pair of squares of different colors. What is the maximum number of pairs that may be removed such that it's always possible to cover the remaining portion of the board with domino pieces?
An Aside
It's a very legitimate question to ask because obviously, at one extreme, when we remove all but two nonadjacent squares, the problem of covering whatever remains will be unsolvable for at least some configurations. On the other hand, as we just saw, removing only two squares we have a solvable problem. Then there must be a borderline number somewhere in between.
At first the problem may seem to be difficult to solve. But you have to start somewhere. As is often the case, experimenting with a few particular cases helps gain insight into a more general problem. So let's start with the next simplest case of four squares (2 white and 2 black) being removed. The forks that worked so well for the previous case become useless. Indeed, following the chain we can remove two consecutive white and two consecutive black squares. This would not yet prove that thus obtained configuration is unsolvable; but doubts that the problem may not have an easy solution may start creeping into your mind. At this point, it may make sense to think of the possibility of a negative result. Can we think of a counterexample? In other words, perhaps it's possible to leave "noncoverable" board by just removing two pairs of squares.
What would make the board noncoverable? Recollecting our original problem, if it were possible to isolate a region of the chessboard that contained an odd number of squares, we would be able to claim that the solution to Problem 3 is 1, just one pair.
Solution
It's possible to remove two pairs of squares as to leave noncoverable chessboard. Indeed, remove two white squares adjacent to a black corner. This creates a region consisting of a single (corner) square that has no adjacent white squares.
Problem 4
Assume we are allowed to remove 2 white and 2 black squares so that the board does not yet fall apart, i.e., does not split into two or more separate pieces. Is it always possible to cover whatever remains of the board with dominoes?
Remark

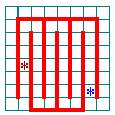
Trying to answer Problem 4 I ran into one noncoverable configuration with 3 pairs of squares removed. The diagram depicts the lower right corner. The red line delineates cut-off squares (3 black and 1 white, the other two white squares have been removed elsewhere.) Blue rectangles denote domino pieces. The right one is forced into its position which in turn forces the next one. The latter blocks a single white square with a cross inside. Thus the configuration is indeed noncoverable. We arrive at the conclusion that a single argument is going to solve both Problems 3 and 4.
Problem 5
This is to check your understanding of the solution to Problem 2.
A rectangular 2nx2m board has been covered with domino pieces. Prove that there exists another cover such that no domino piece belongs to both covers.
Perhaps surprisingly, covering a chessboard with dominoes raises a few more interesting questions.
Reference
- P. J. Davis and R. Hersh, The Mathematical Experience, Houghton Mifflin Company, Boston, 1981
- R. Honsberger, Mathematical Gems II, MAA, New Math Library, 1976
- M. Kac and S. M. Ulam, Mathematics and Logic, Dover Publications, NY, 1968.
- A. Soifer, Geometric Etudes in Combinatorial Mathematics, Springer, 2010 (2nd, expanded edition)
|Contact| |Front page| |Contents| |Algebra| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73575027
