Covering a Chessboard with a Hole with L-Trominoes

The applet below is an interactive illustration for the problem #678 proposed by Charles W. Trigg, San Diego, California (Mathematics Magazine, Vol. 41, No. 1 (Jan., 1968), p. 42):

From an 8 by 8 checkerboard, the four central squares are removed.

  1. Show how to cover the remainder of the board with right trominoes so as to have no fault line, or exactly two fault lines, or three fault lines.
  2. Show that no covering with right trominoes can have four fault lines.

A right tromino is a nonrectangular assemblage of three adjoining squares mostly referred to as L-tromino at this site. A fault line has its extremities on the perimeter so that a portion of the configuration may be slid along it in either direction without otherwise disturbing the relative position of its parts.

(Two draw a tromino, click on one of the squares, move (not drag) the cursor to the next one and click again, move to a third (suitable) square and - to place a tromino - click the third time.)

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

Golomb's theory assures us that the 8×8 board with a 2×2 hole - whenever the latter is cut off - can be covered with L-trominoes and that in multiple ways. Indeed, place one tromino into the cut-off square will leave a 1×1 hole. Now Golomb's theorem shows that an 8×8 board with a 1×1 hole can be covered with L-trominoes. So the question is clearly about counting the fault lines.

Solution


Related material
Read more...

  • Covering A Chessboard With Domino
  • Dominoes on a Chessboard
  • Tiling a Chessboard with Dominoes
  • Vertical and Horizontal Dominoes on a Chessboard
  • Straight Tromino on a Chessboard
  • Golomb's inductive proof of a tromino theorem
  • Tromino Puzzle: Interactive Illustration of Golomb's Theorem
  • Tromino as a Rep-tile
  • Tiling Rectangles with L-Trominoes
  • Squares and Straight Tetrominoes
  • Tromino Puzzle: Deficient Squares
  • Tiling a Square with Tetrominoes Fault-Free
  • Tiling a Square with T-, L-, and a Square Tetrominoes
  • Tiling a Rectangle with L-tetrominoes
  • Tiling a 12x12 Square with Straight Trominoes
  • Bicubal Domino

    • |Contact| |Front page| |Contents| |Games|

    Copyright © 1996-2018 Alexander Bogomolny

    Solution

    Solution below is by Benjamin L. Schwartz, The MITRE Corporation, Virginia.

    The problem as stated leaves unsettled the question of the existence of exactly one fault line. In the discussion below, we shall also resolve this question affirmatively with an example.

    Notation. Denote the 8 horizontal rows of squares by letters A through H. Denote the vertical files by numbers 1 through 8. Denote a line between rows by the names of the two bordering rows (e.g., line BC).

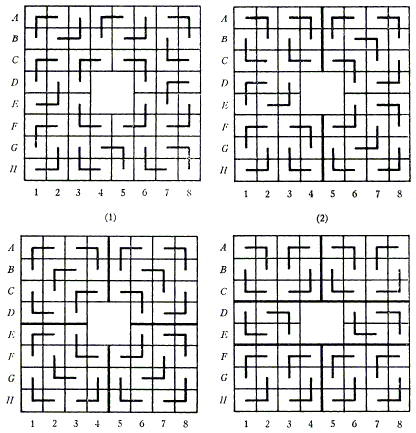
    1. The diagrams (1), (2), (3) and (4) show examples with zero, one, two and three fault lines, respectively. In (2), the fault line is 34. In (3), the fault lines are DE and 45; and, in (4), they are CD, EF and 45. As shown later, these arrangements of fault lines are essentially unique.

    2. To prove other cases impossible, we introduce a few easily proved lemmas about coverings with trominoes. Proofs are omitted.

      1. A 2×n area can be covered iff 31 n.
      2. Two adjacent lines (e.g., CD and DE) cannot both be fault lines.
      3. A 3×3 area cannot be covered exactly.
      4. A fault line cannot occur adjacent to an edge.

    Lemma IV eliminates A F, GH, 12 and 78 as candidates. But Lemma I also eliminates BC, FG, 23 and 67. Hence the only horizontal candidates are CD, DE and EF; and verticals 34, 45 and 56. Furthermore, by Lemma II, if DE is a fault line, it is the only horizontal one. Similarly, if 45 is a vertical fault line, it is the only one.

    Thus, the only prospect for a 4-fault-line configuration requires that these lines be CD, EF, 34 and 56. But this means the 3×3 areas in the four corners must be covered exactly, which violates Lemma III. An additional question is whether the arrangement of fault lines in each of the various cases is essentially unique. The affirmative answer to this follows from the following theorem:

    If CD is a fault line, so is EF. (Similarly 34 and 56.)

    To see this, suppose there is a covering with CD as a fault line. Then consider how square Dl could be covered. Place a tromino to cover it with each of the three possible orientations of the other two squares. It follows that either the other squares of files 1 and 2 in rows D and E cannot be covered, or can only be covered in such a way as to fill exactly the 2×3 rectangle (123)×(DE). The same argument applies to (678)×(DE). Hence EF must be a fault line.

    A more laborious and detailed analysis concerns the actual arrangement of the trominoes in the coverings. It has shown that except for "flipover" of the coverings of 2×3 rectangles, and rotations of the entire board, the solutions of (2), (3) and (4) are unique. A similar statement is believed to hold for (1), but has not yet been proved.

    |Contact| |Front page| |Contents| |Games|

    Copyright © 1996-2018 Alexander Bogomolny

    71537313