Construction of n-gon from the midpoints of its sides

Construct an n-gon (polygon with n sides) for which n given points serve as midpoints of its sides.

Below there is a Java applet that may help you gain insight into the problem. The applet can be in two modes: "Place points" and "Drag mouse", depending on which of the two boxes at the bottom of the applet is checked.

• In the "Place points" mode you should define n points - midpoints of the sides of a polygon. Just click the mouse anywhere inside the applet's rectangle.
• Next you can experiment with the points you thus defined. Change the mode and start dragging the mouse.

If, for whatever reason, you decide to work with a different set of points - press the Reset button and start again.

A word of advice. First of all, start with a simple case. Try just a few points, say, 3, 4, 5. Secondly, attempt to visualize a polygon and then place the points approximately at the middle of its sides. Thirdly, pay attention to the red "target" circle.

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

Buy this applet What if applet does not run?

By now you ought to have arrived at the following conclusions:

• If n is odd it's probably possible to solve the problem.
• If n is even something goes wrong.

For odd n, the red circle indicates one of the polygon's vertices. Once you move the cursor into the red circle the problem seems to have been solved. Now, actually the applet provides an experimental device. It may help you to fathom a proof but it can't substitute for a rigorous demonstration.

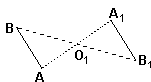
Useful for the proof could be the following observation: Let there be given a segment AB and a point O₁. Consider a reflection A₁B₁ of AB in the point O₁. In other words, in order to obtain A₁B₁ rotate AB around O₁ 180^o. Now AB || A₁B₁ but they have a different orientation. If you continue reflecting A₁B₁ in another point O₂ to get A₂B₂ then the segments remain parallel and equal but orientation changes again. After an odd number (1 in particular) of reflections the last segment will be parallel to AB but having a different orientation. After an even number of reflections the first and the last segment will be directly parallel (and, of course, equal). See if you can now complete the proof.

Remark 1

When n is even the segment joining the first and the last point is always the same for a given configuration of vertices. For n = 4, the two points coincide iff the vertices form a parallelogram and are ordered along its boundary. This reflects on the Varignon's theorem. (See, C. Pritchard, The Changing Shape of Geomtetry, Cambridge University Press, 2003, p. 177). If the segment in question degenerates into a point, the problem has infinitely many solutions. Otherwise, no solution exists.

Remark 2

The problem could be described algebraically. Assume m_i, i = 1, 2, ..., n, stand for the vectors from the origin to the given midpoints. (We may also treat them as the points in an affine space.) Let a_i, i = 1, 2, ..., n, denoted the unknown vertices. Then a_i's satisfy the following system of equations:

Surprisingly this same system of equations describes an apparently unrelated problem.

|Contact| |Front page| |Contents| |Eye opener| |Geometry| |Store|

But before we do, let's create an accurate picture of what happened. Three successive reflections resulted in another reflection. And the same is probably true of any odd number of reflections. Reflections are just functions: they map points of a plane into points of the same plane. Successive application of two reflections is none other than the composition of the corresponding functions. Thus we want to show that composition of an odd number of reflections is again a reflection.

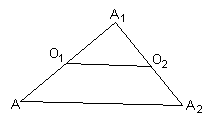
What about an even number of reflections? What about just two reflections? Composition of two reflections is a translation to the vector parallel to the line connecting the two centers of reflection and twice as long as the distance between the centers. Indeed, in ΔAA₁A₂, AO₁ = O₁A₁ and A₁O₂ = O₂A₂. Therefore, triangles AA₁A₂ and O₁A₁O₂ are similar and AA₂ = O₁O₂.

Translation is a transformation of a plane that moves the plane as a whole in a certain direction to a certain distance. Each point is shifted by a certain vector. Composition of two translations with vectors v₁ and v₂, respectively, is again a translation corresponding to the vector sum v₁ + v₂. The latter remark easily leads to a solution of our problem for an even number of points. If n is even, we can combine successive reflections in pairs to get n/2 successive translations. Obviously (e.g., by induction) the sum of any number of translations is a translation. This is true as long as we may refer to the triangular diagram above. But sometimes the sum of vectors is 0 (one side of a triangle shrinks to a point, and the triangle does not appear triangular in the least.) To make the italicized statement universally true we have to accept as a translation the identical transformation under which every point is mapped onto itself. The identical transformation has all points fixed. Since any translation moves all points by the same vector, the only translation that has a fixed point is identical.

Returning to our problem for n even. Let vectors v_i, i = 1,...,n/2 map, respectively, O₁ to O₂ (i = 1), O₃ to O₄ (i = 2), ..., O_n-1 to O_n (i = n/2). Consider two cases:

1. v₁ + v₂ + ... + v_n/2 = 0, and
2. v₁ + v₂ + ... + v_n/2 ≠ 0.

In case 1, pick any point A and obtain points A_i by successive reflections in points O_i. Then A_2n will coincide with A thus solving the problem. Since A is arbitrary, the problem has an infinite number of solutions.

In case 2, no solution exists.

For n odd, the problem always has a unique solution. As we already noticed, we have to show that the composition of an odd number of reflections is again a reflection. Taking the center of the latter as a starting point A which is successively reflected in points O_i we'll find that the point A_n coincides with A. To prove the statement, note that (by induction) composition of an odd number of reflections is the composition of a reflection and a translation (or of a translation and a reflection depending on how one groups our reflections.)

Choose two points A and B, shift them into A₁ and B₁ by vector v, and then reflect these two in a point O to obtain A₂ and B₂. As we already know, the quadrilateral ABA₂B₂ is a parallelogram. Let P denote the point of intersection of its diagonals. This is the midpoint of the segment AA₂. Now let B vary. Regardless of its position, the midpoint of the segment BB₂ will always coincide with the midpoint of AA₂, that is P. Therefore, B₂ is always obtained from B by reflection in P.

From the above discussion it follows that all planar translations form a group, and another group is formed by all translations and reflections. The group of translations is commutative (Abelian); for the sum of vectors is commutative. The combined group of translations and reflections is not commutative. It can be shown (try it) that, in general, the composition TR of a translation T and a rotation R is not the same as RT.

|Contact| |Front page| |Contents| |Eye opener| |Geometry| |Store|