Varignon Parallelogram: What is it?
A Mathematical Droodle
14 December 2015, Created with GeoGebra
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyVarignon Parallelogram
Midpoints of successive sides of a quadrilateral form a parallelogram. To see this, observe that the lines in question are parallel to the diagonals of the quadrilateral. They are therefore pairwise equal and parallel. This is known as the Varignon parallelogram.
The two lines that join the midpoints of the opposite sides of the quadrilateral serve as the diagonals of the Varignon parallelogram. They are divided into halves by their point of intersection. (In 3D, a similar result holds for the three lines connecting the midpoints of the opposite edges of a tetrahedron: the three are concurrent. The common point serves as the center of gravity of the four vertices. The center of gravity divides each of the three lines into two equal parts.)
Coxeter and Greitzer attribute the theorem to Pierre Varignon (1654-1722). The theorem was published posthumously in 1731. Given its simplicity, it is utterly surprising that it had to be waiting that long to be discovered.
The area of Varignon's parallelogram is one half that of the quadrilateral. This is how you can see it.
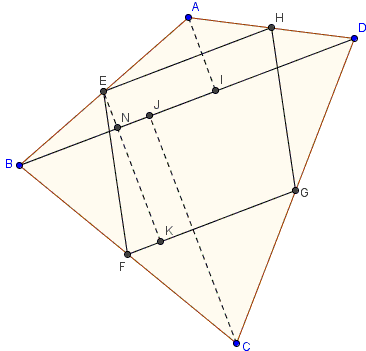
With a reference to the above disgram,
$\begin{align} \mbox{Area}(EFGH) &= EK\cdot FG\\ &= (EN+KN)\cdot\frac{1}{2}BD\\ &= \frac{1}{2}BD\cdot EN+\frac{1}{2}BD\cdot KN\\ &= \frac{1}{4}BD\cdot AI+\frac{1}{4}BD\cdot CJ\\ &= \frac{1}{2}\mbox{Area}(ABD)+\frac{1}{2}\mbox{Area}(BCD)\\ &= \frac{1}{2}\mbox{Area}(ABCD). \end{align}$
The perimeter Varignon's parallelogram is equal to the sum of the diagonals of the quadrilateral. There is a later page with a proof without words.
The Varignon parallelogram, together with a construction that leads to the Parahexagon, admits a simple generalization.
The diagonals of Varignon's parallelgrams join the midpoints of the opposite sides of the quadrilateral. These are known as its bimedians. It follows that in any quadrilateral the bimedians are halved by their intersection point.
References
- C. Alsina, R. B. Nelsen, Charming Proofs, MAA, 2010, pp. 107-108
- J. Casey, A Sequel to Euclid, Scholarly Publishing Office, University of Michigan Library (December 20, 2005), reprint of the 1888 edition
- H.S.M. Coxeter, S.L. Greitzer, Geometry Revisited, MAA, 1967, p. 53
- S. Rabinowitz (ed), Problems and Solutions from the Mathematical Visitor (1877-1896), MathPro Press, 1996, #151
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2018 Alexander Bogomolny73558764
