Equilateral Triangle on Parallel Lines

Construct an equilateral triangle whose vertices lie on three parallel lines (one vertex per line.)

In the applet below, each of the parallel lines can be dragged up or down. There are draggable points C, C₁, and C₂, one per line. The question is to position them so as to get an equilateral triangle.

Solution

|Activities| |Contact| |Front page| |Contents| |Geometry| |Eye opener| |Store|

Copyright © 1996-2012 Alexander Bogomolny

Construct an equilateral triangle whose vertices lie on three parallel lines (one vertex per line.)

The problem illustrates an application of the Rotation Transform.

Let L be the line that bears point C, and similarly L₁ and L₂.

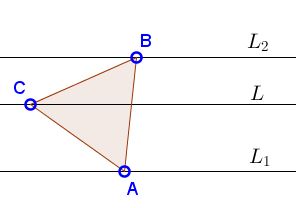
Assume ΔABC is equilateral, with A on L₁ and B on L₂. Rotation through 60° around C maps A on B. (The rotation may be either clockwise or counterclockwise depending on the orientation of ΔABC. Generally speaking the problem admits two solutions differently oriented.) Let's perform such a rotation: rotate line L₁ through 60° into position L'. The image of A under that rotation lies on L' but also coincides with B. It follows that B is the intersection of L' with L₂ and A the corresponding point on L₁.

This leads to the following construction: rotate L₁ around C though 60° into position L'. Denote B the intersection of L' and L₂ and A the inverse rotation of B. Then ΔABC is equilateral,scalene,right,equilateral,obtuse.

For proof, observe that by the construction CA = CB and ∠ACB = 60°.

References

1. I. M. Yaglom, Geometric Transformations I, MAA, 1962, Chapter 2, Problem 18

|Activities| |Contact| |Front page| |Contents| |Geometry| |Eye opener| |Store|

Copyright © 1996-2012 Alexander Bogomolny