Three Tangents Theorem
What is this about?
A Mathematical Droodle
Explanation
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
The notations used in the applet are reminiscent of a different result where the diagram is almost the same. There is just one difference: the point W there has been moved to infinity. The statement is actually simplified:
| (1) |
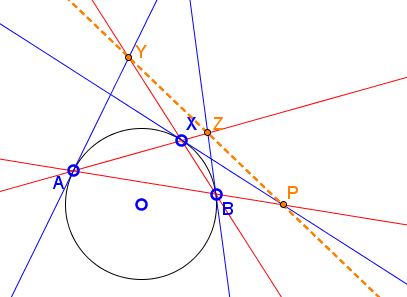
Let TA, TX, and TB be the tangents to the circumcircle of ΔAXB at vertices A, X, and B respectively. Assume that BX and AX produced beyond X intersect TA and TB in Y and Z, respectively. Assume also that TX meets TA in U and TB in V. Then the three lines TX, UV, and AB are either parallel or concurrent.
|
The three lines could be parallel iff X is the midpoint of the arc AXB. In this case, the lines are parallel because of the symmetry of the configuration. However, the above statement is conspicuously asymmetric with regard to the vertices of the triangle. The vertex X has been singled out in that the corresponding tangent TX plays a role different from that of the other two, TA and TB, which prompts a second look at the diagram.
In fact, the vertices of ΔAXB, besides P, there are other two points through which pass three lines: Y and Z. It's not hard to see that those points play the role of P under permutation of the vertices. The three points P, Y, Z have a few things in common:
P, Y, Z are collinear.
Each is found at the intersection of one of the tangents with the opposite side line of ΔAXB.
Thus we come up with a reformulation in which the vertices of the triangle play similar roles:
| (2) |
Let TA, TX, and TB be the tangents to the circumcircle of ΔAXB at vertices A, X, and B respectively. Let points Y, P, and Z denote the points of intersection of the tangents with the opposite side lines of ΔAXB. Then the three points P, Y, Z are collinear.
|
This is the statement I am going to prove.
Proof
For the proof note that regardless of how the points P, Y, Z have been obtained, the lie one on each side line of ΔAXB. We are to prove that the points are collinear. This calls for the converse of Menelaus' theorem. According to the latter, (2) will follow from
| (3) |
AP/BP·BY/XY·XZ/AZ = 1,
|
where the segments involved are thought to be signed.
To deal with the first ratio, AP/BP, we note a pair of similar triangles. In ΔAXP and ΔXBP that share angle at P, we also have
For, ∠XAP (= ∠XAB) subtends the same arc as is enclosed into by ∠BXP formed by chord AB and the tangent TB at B. From the similarity of the triangles we derive:
AP/XP = XP/BP = AX/XB,
from which it follows that
| (5P) |
AP/BP = AP/XP·XP/BP = AX2/XB2.
|
Similarly we obtain
| (5Y) | BY/XY = AB2/AX2 |
| (5Z) | XZ/AZ = XB2/AB2, |
so that (3) follows from (5P), (5Y), (5Z).
The above configuration of a triangle and the tangents to its circumcircle at the vertices is quite remarkable in many other respects. The triangle formed by the lines TA, TX and TB is known as the tangential (or contact) triangle of the reference ΔAXB. By definition, the circumcircle of ΔAXB is simultaneously the incircle of its tangential triangle. Since, a symmedian through a vertex passes through the point of intersection of the tangents to the circumcircle at the other two vertices, its Lemoine point also serves as the Gergonne point of the tangential triangle.
The line YZP is known as the Lemoine line of ΔAXB. It's the polar of the Lemoine point with respect to the circumcircle. This is the Gergonne line of the tangential triangle.
Symmedians through vertices of ΔAXB pide the opposite sides in exactly the proportions (5P), (5P), (5Z). For this reason, the tangents TA, TX and TB are often called external symmedians of ΔAXB. The points of intersection of the internal and external symmedians through the same vertex with the opposite side are harmonic conjugates of each other with respect to the other two vertices.
The points Y, Z, and P are known as Nobbs' points of ΔAXB.
Finally, the Three Tangents Theorem has a more general formulation.
References
- F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991, pp. 1175-1177
- R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, 1995, pp. 151-153
- R. Honsberger, In Pólya's Footsteps, MAA, 1997, pp. 175-176
Symmedian
- All about Symmedians
- Symmedian and Antiparallel
- Symmedian and 2 Antiparallels
- Symmedian in a Right Triangle
- Nobbs' Points and Gergonne Line
- Three Tangents Theorem
- A Tangent in Concurrency
- Symmedian and the Tangents
- Ceva's Theorem
- Bride's Chair
- Star of David
- Concyclic Circumcenters: A Dynamic View
- Concyclic Circumcenters: A Sequel
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
|
