Two Perspective Triangles
Given ΔABC, the medial triangle MaMbMc joins the midpoints of its sides, while the orthic triangle HaHbHc joins the feet of its altitudes. Triangles ABC and MaMbMc are homothetic in their common centroid, such that all of their remarkable points, lines and triangles are also homothetic. As a weak consequence, the corresponding objects of a triangle and its medial triangle are perspective. In particular, this is true for their orthic triangles.
Vladimir Nikolin observed (June, 2012) a simple, yet a non-trivial fact:
The medial triangles of a triangle and of its orthic triangle are perspective.
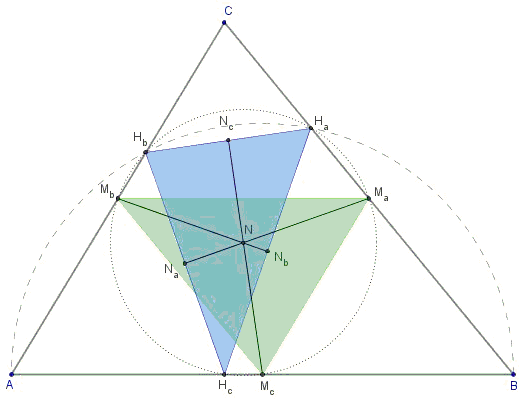
In other words, lines MaNa, MbNb, McNc, where Na, Nb, and Nc are the midpoints of the orthic triangle HaHbHc, are concurrent. Furthermore, they are concurrent in the 9-point center of ΔABC.
Proof
As the feet of two altitudes, Ha and Hb lie on the semicircle centered at Mc, implying that
Nine Point Circle
- Nine Point Circle: an Elementary Proof
- Feuerbach's Theorem
- Feuerbach's Theorem: a Proof
- Four 9-Point Circles in a Quadrilateral
- Four Triangles, One Circle
- Hart Circle
- Incidence in Feuerbach's Theorem
- Six Point Circle
- Nine Point Circle
- 6 to 9 Point Circle
- Six Concyclic Points II
- Bevan's Point and Theorem
- Another Property of the 9-Point Circle
- Concurrence of Ten Nine-Point Circles
- Garcia-Feuerbach Collinearity
- Nine Point Center in Square
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73576473
