Sequences of Concyclic Points on a Conic

Let $ABCD,$ $BNPC,$ and $MADQ$ be cyclic quadrilaterals. Assume that points $A,B,C,D,M,N,P,Q$ are on a conic.

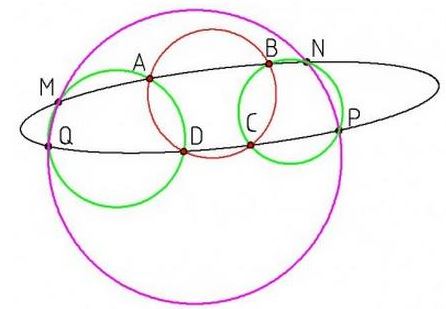
concyclic points on a conic

Prove that: $M,N,P,Q$ are concyclic.

Recollect, for a proof, that under the conditions of the statement, $NP\parallel AD$ and $BC\parallel MQ.$ Consider circumcircle $(MNP)$ and its fourth intersection $Q'$ with the conic. By the same earlier theorem, $MQ'\parallel BC$ which of course implies $Q=Q'$ thus proving the current statement.

The combination of the two theorems begs for a generalization:

Assume for integer $n\ge 3,$ points $A_{i}, B_{i},$ $i=1,\ldots ,n,$ lie on a conic. Assume also that the quadrilaterals $A_{i}A_{i+1}B_{i+1}B_{i},$ $i=1,\ldots,n-1$ are cyclic. Then, for odd $n,$ $A_{n}B_{n}\parallel A_{1}B_{1};$ whereas for even $n,$ the quadrilateral $A_{1}A_{n}B_{n}B_{1}$ is cyclic.

The question has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page.

72393128