Ceva's theorem applies to a configuration of three concurrent cevians in a triangle. Hiroshi Haruki made an observation that a similar fact holds in some circumstances when an actual triangle is missing. More accurately, it is known that the common chords of three intersecting circles meet in the radical center of the circles.

The three concurrent "cevians" are present, but where is the triangle? The common points of the circle can still be connected to form a 3-prodded star, the lengths of whose sides we denote successively a, b, c, d, e, f.

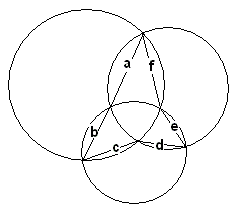
Professor Haruki observed that the six lengths satisfy a Ceva-like identity:

To see why this is so, introduce three additional lengths x, y, z, as in the diagram:

Now imagine the circles separated, each with the inner chords intact. The chords will naturally be inherited by two circles.

Because of the properties of inscribed angles, the chords in each of the circles form similar triangles. We thus derive three proportions:

the product of which gives exactly (1).

References

1. R. Honsberger, The Butterfly Problem and Other Delicacies from the Noble Art of Euclidean Geometry I, TYCMJ, 14 (1983), pp. 2-7.

Copyright © 1996-2009 Alexander Bogomolny