Problem 790 from Pentagon: an Inequality in Two Variables
Problem
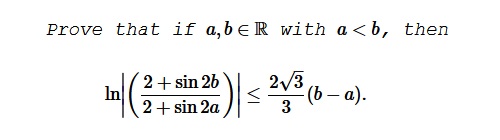
Solution 1
$\displaystyle \begin{align} \cos \Bigr(2x+\frac{\pi}{6}\Bigr)\leq 1&\Leftrightarrow \frac{\sqrt{3}}{2}\cos 2x-\frac{1}{2}\sin 2x\leq 1\\ &\Rightarrow \int_a^b \frac{2 \cos 2x}{2+\sin 2x}dx\leq \int_a^b \frac{2\sqrt{3}dx}{x}\\ &\Leftrightarrow [\ln |2+\sin 2x|]_a^b\leq \frac{2\sqrt{3}}{3}(b-a)\\ &\Leftrightarrow \ln \Bigr|\frac{2+\sin 2b}{2+\sin 2a}\Bigr|\leq \frac{2\sqrt{3}}{3}(b-a) \end{align}$
Solution 2
Let $f(x)=\ln (2+\sin 2x), x\in \mathbb{R}.$ Then
$\displaystyle \begin{align} f'(x)&=\frac{2\cos 2x}{2+\sin 2x}\\ f''(x)&=2\frac{(-2\sin 2x)(2+\sin 2x)-(2\cos 2x)\cos 2x}{(2+\sin 2x)^2}\\ &=(-4)\cdot \frac{2 \sin 2x+1}{(2+\sin 2x)^2} \end{align}$
$\displaystyle \begin{align} f''(x)&=0\Leftrightarrow \sin 2x=-\frac{1}{2}=\sin \Bigr(\frac{7\pi}{6}\Bigr)\\ &\Leftrightarrow 2x=n\pi +(-1)^n \Bigr(\frac{7\pi}{6}\Bigr), n\in \mathbb{Z}\\ &\Leftrightarrow x=n\Bigr(\frac{\pi}{2}\Bigr)+(-1)^{n+1}\frac{\pi}{12}, n\in \mathbb{Z} \end{align}$
Thus,
$\displaystyle\begin{align} \max f'(x)&=\max \left\{f'\left(\frac{7\pi}{12}\right), f'\left(\frac{11\pi}{12}\right),f' \left(\frac{19\pi}{12}\right),\ldots \right\}\\ &=\max \left\{f'\left(\frac{7\pi}{12}\right), f'\left(\frac{11\pi}{12}\right)\right\}\\ &=\frac{2}{\sqrt{3}}\\ \min f' (x)&=-\frac{2}{\sqrt{3}}. \end{align}$
By the first mean value theorem, for $a\lt b,$
$\displaystyle \begin{align} \frac{f(b)-f(a)}{b-a}=f'(c),\, \textit{ for some }\,c\in (a,b)&\Rightarrow\\ \ln \Bigr(\frac{2+\sin 2b}{2+\sin 2a}\Bigr)=f'(c)(b-a)&\Rightarrow\\ \Bigr|\ln \Bigr(\frac{2+\sin 2b}{2+\sin 2a}\Bigr)\Bigr|=|f'(c)|(b-a)\leq \frac{2}{\sqrt{3}}(b-a). \end{align}$
Solution 3
Let $f(x)=\ln \left(2+\sin (2x)\right).$ Clearly, $f$ is differentiable on $\mathbb{R}$ and we have
$\displaystyle \begin{align} f'(x)&=\frac{2\cos (2x)}{2+\sin (2x)}\\ f''(x)&=-4\cdot \frac{1+2\sin (2x)}{(\sin (2x)+2)^2} \end{align}$
Now, $f''$ vanishes at $\displaystyle x_0=-\frac{\pi}{12} (\mod \pi).$ Hence, $f'$ has a maximum at $\displaystyle x_0=-\frac{\pi}{12}$ and we have $\forall x\in \mathbb{R},$ $\displaystyle |f'(x)|\leq \frac{2\sqrt{3}}{3}.$
Using the Lagrange's theorem, there is $c\in (a,b)\quad [\textit{for sure } a,b\in \mathbb{R}]$ such that $\displaystyle \frac{f(b)-f(a)}{b-a}=f'(c)$ hence we conclude that $\displaystyle |f(b)-f(a)|\leq \frac{2\sqrt{3}}{3}|f'(c)|$ or $\displaystyle \left|\ln \left(\frac{2+\sin (2b)}{2+\sin (2a)}\right)\right|\leq \frac{2\sqrt{3}}{3}|b-a|$ and we are done.
Solution 4
Let $f(x)=\ln |2+\sin 2x|,$ $\displaystyle f'(x)=\frac{2\cos 2x}{2+\sin 2x}.$ By Lagrange's theorem, $f(b)-f(a)=f'(c)(b-a),$ with $c\in (a,b).$ Specifically,
$\displaystyle \ln \left|\frac{2+\sin 2b}{2+\sin 2a}\right|\leq \frac{2\cos 2c}{2+\sin 2c}(b-a)$
We need to prove that
$\displaystyle \begin{align} \frac{2\cos 2c}{2+\sin 2c}\leq \frac{2\sqrt{3}}{3}&\Leftrightarrow \sqrt{3}\cos 2c-\sin 2c\leq 2\\ &\Leftrightarrow \cos \left(2c+\frac{\pi}{6}\right)\leq 1. \end{align}$
True.
Solution 5
The given inequality transforms into:
$\displaystyle \begin{align} &\ln |2+\sin 2b|-\ln |2+\sin 2a|\leq \frac{2\sqrt{3}}{3}(b-a)\\ &\Leftrightarrow \ln (2+\sin 2b)-\ln (2+\sin 2a) \overbrace{\leq}^{(a)}\frac{2\sqrt{3}}{3}(b-a) \end{align}$
(for $2+\sin 2t\geq 1\gt 0\;\forall t\in \mathbb{R},$ as $-1\leq \sin 2t \leq 1).$
Let $f(x)=\ln (2+\sin 2x).$ Then $\displaystyle (a) \Leftrightarrow f(b)-f(a)\leq \frac{2\sqrt{3}}{3}(b-a).$
Clearly, $f(x)$ is continuous and differentiable on any interval $(a,b).$ Therefore, using Lagrange's Mean Value Theorem, there exists a value $c \ in (a,b),$ such that $\displaystyle f'(c)=\frac{f(b)-f(a)}{b-a}.$ Now, with
$\displaystyle g(x)=f'(x)=\frac{2\cos (2x)}{\sin 2x+2},$ $\displaystyle g'(x)=-\frac{4(1+2\sin 2x)}{(\sin 2x+2)^2},$ and $\displaystyle g''(x)=\frac{(16\cos 2x)(\sin 2x-1)}{(\sin 2x+2)^3}.$
Now, $g'(x)=0$ when $\displaystyle \sin 2x=-\frac{1}{2}$ and $\displaystyle \cos 2x=\pm \frac{\sqrt{3}}{2}.$
When $\displaystyle \sin 2x=-\frac{1}{2}$ and $\displaystyle \cos 2x=\frac{\sqrt{3}}{2},$ $g''(x)\lt 0,$ implying $f(x)$ attains maxima, and, when $\displaystyle \sin 2x =-\frac{1}{2}$ and $\displaystyle \cos 2x=-\frac{\sqrt{3}}{2},$ $g''(x)\gt 0,$ implying $f(x)$ attains minima. Therefore
$\displaystyle g(x)_{\max} =\frac{2(\frac{\sqrt{3}}{2})}{2-\frac{1}{2}}=\frac{\sqrt{3}}{\frac{3}{2}}\overbrace{=}^{(3)} \frac{2\sqrt{3}}{3} $
From (1), (2), (3), it follows that
$\displaystyle\frac{f(b)-f(a)}{b-a}\leq \frac{2\sqrt{3}}{3}\Rightarrow f(b)-f(a)\leq \frac{2\sqrt{3}}{3}(b-a),$
because $b-a\gt 0.$
Solution 6
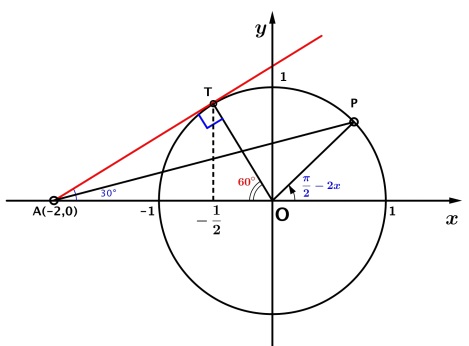
Let $\displaystyle \angle POx=\frac{\pi}{2}-2x$ for $\displaystyle P\left(\cos \left(\frac{\pi}{2}-2x\right)\right).$ We see that the slope of $AP$ is less than that of $AT.$ So that
$\displaystyle \frac{\sin (\frac{\pi}{2}-2x)}{\cos (\frac{\pi}{2}-2x)+2}\leq \frac{1}{\sqrt{3}}.$
Therefore
$\displaystyle \int_a^b \frac{2\cos 2x}{2+\sin 2x}dx\leq \int_a^b \frac{2}{a\sqrt{3}}dx\Leftrightarrow [\ln |2+\sin x|]_a^b \leq \frac{2}{\sqrt{3}}(b-a)$
Solution 7
Condition $a\lt b$ is unnecossary. Let $f(x)=\ln(2+\sin 2x).$ Then $\displaystyle |f(b)-f(a)=\frac{2|\cos 2c|}{2+\sin 2c}\cdot |b-a|.$ Hence, suffice it to show that $\displaystyle\frac{2|\cos 2c|}{2+\sin 2c}\le\frac{2}{\sqrt{3}}$ which is equivalent to $-\sin 2c\pm\sqrt{3}\cos 2c\le 2.$ That can be verified by squaring or with the Cauchy-Schwarz inequality.$
Acknowledgment
I could not be more grateful to Dan Sitaru who has kindly communicated to me the problem with several solutions on a LaTeX file. Solution 1 is by Abdelhak Maoukouf (Casablanca, Morocco); Solution 2 by Ravi Prakash (New Delhi, India); Solution 3 by Anas Adlany (El Zemamra, Morocco); Solution 4 by Richdad Phuc (Hanoi, Vietnam); Solution 5 by Soumava Chakraborty (Kolkata, India); Solution 6 by Kunihiko Chikaya (Tokyo, Japan); Solution 7 by Leo Giugiuc (Drobeta-Turnu Severin, Mehedinti, Romania).
Inequalities in Two Variables
- An Inequality with Just Two Variable $\left(\displaystyle\left(\frac{2ab}{a+b}+\sqrt{\frac{a^2+b^2}{2}}\right)\left(\frac{a+b}{2ab} + \sqrt{\frac{2}{a^2+b^2}}\right) \le \frac{(a+b)^2}{ab}\right)$
- An Inequality with Just Two Variable II $\left(\displaystyle\small{\left(\frac{2ab}{a+b}+\sqrt{ab}+\frac{a+b}{2}\right)\left(\frac{a+b}{2ab} + \frac{1}{\sqrt{ab}}+\frac{2}{a+b}\right) \le 5 +2 \left(\frac{a}{b}+\frac{b}{a}\right)}\right).$
- An Inequality with Just Two Variable III $\left(\displaystyle\frac{a}{b\sqrt{2}}+\frac{b\sqrt{2}}{a}+2\left(\frac{\sqrt{a^2+b^2}}{b}+\frac{b}{a^2+b^2}\right)\ge \frac{9\sqrt{2}}{2}\right)$
- An Inequality with Just Two Variables IV $\left(\displaystyle\frac{a+2}{a^2+a+1}+\frac{b+2}{b^2+b+1}\ge \frac{ab+2}{(ab)^2+ab+1}+1\right)$
- An Inequality with Just Two Variables V $\left(\displaystyle \left(\ln\left(\frac{1}{2a}+\frac{1}{2b}\right)\right)^{a+b}\ge \left(\ln\frac{1}{a}\right)^b\left(\ln\frac{1}{b}\right)^a\right)$
- An Inequality with Just Two Variables VI $\left(|x-y|(x+1)(y+1)\le 2\right)$
- An Inequality with Just Two Variable VII $\left(\displaystyle (x^3+y^3)^3(x^2-xy+y^2)\ge x^2y^2\sqrt{xy}(x^2+y^2)^3\right)$
- An Inequality with Just Two Variable VIII $\left(\displaystyle \frac{a^2}{b+2}+\frac{b^3}{a+2}+(2-a)b^2\le 12\right)$
- The power of substitution III: proving an inequality with two variables $\left(\displaystyle\frac{1}{\sqrt{1+a^2}}+\frac{1}{\sqrt{1+b^2}}\le\frac{2}{\sqrt{1+ab}}\right)$
- Simple Yet Uncommon Inequalities with Absolute Value $\left((|x|-|y|)^2\le |x^2-y^2|,\,|\sqrt{|x|}-\sqrt{|y|}|\le\sqrt{|x-y|}\right)$
- An Inequality with Just Two Variable And an Integer $\small{\left(\displaystyle \Bigr(\frac{a}{b^n}+\frac{b}{a^n}\Bigr)\Bigr(\frac{a^n}{b}+\frac{b^n}{a}\Bigr)\Bigr(\frac{a^n}{b^n}+\frac{b}{a}\Bigr)\Bigr(\frac{b^n}{a^n}+\frac{a}{b}\Bigr)\geq 8\left(\sqrt{\displaystyle\left(\frac{a}{b}\right)^{n-1}}+\sqrt{\displaystyle\left(\frac{b}{a}\right)^{n-1}}\right)\right)}$
- An Inequality with Exponents $\left(\displaystyle b^b\cdot e^{a+\frac{1}{a}}\ge 2e^b\right)$
- Problem 790 from Pentagon: an Inequality in Two Variables $\left(\displaystyle\ln \left|\left(\frac{2+\sin 2b}{2+\sin 2a}\right)\right|\leq \frac{2\sqrt{3}}{3}(b-a)\right)$
- An Inequality with Two Variables from Awesome Math $\left(\displaystyle \frac{6ab-b^2}{8a^2+b^2}\lt\sqrt{\frac{a}{b}}\right)$
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73581996
