An Inequality with Just Two Variables II
Problem
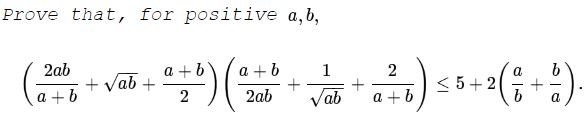
Solution 1
$\displaystyle\begin{align} LHS &= 3+\frac{4\sqrt{ab}}{a+b}+\frac{a+b}{\sqrt{ab}}+\frac{4ab}{(a+b)^2}+\frac{(a+b)^2}{4ab}\\ &\le 3+2+\frac{a+b}{\sqrt{ab}}+1+\frac{(a+b)^2}{4ab}\\ &= 6+\frac{a+b}{\sqrt{ab}}+\frac{(a+b)^2}{4ab}. \end{align}$
Suffice it to show that
$\displaystyle 6+\frac{a+b}{\sqrt{ab}}+\frac{(a+b)^2}{4ab}\le 5 +2 \left(\frac{a}{b}+\frac{b}{a}\right)$
which is equivalent to
(1)
$\displaystyle 1+\frac{a+b}{\sqrt{ab}}+\frac{(a+b)^2}{4ab}\le \frac{2(a^2+b^2)}{ab}.$
Now, by the GM-HM inequality, $\displaystyle\sqrt{ab}\ge\frac{2ab}{a+b},\;$ hence $\displaystyle\frac{a+b}{\sqrt{ab}}\le\frac{(a+b)^2}{2ab}.$
It follows that
(2)
$\displaystyle \frac{a+b}{\sqrt{ab}}+1+\frac{(a+b)^2}{4ab}\le 1+\frac{3(a+b)^2}{4ab}.$
(1) and (2) show that the problem will be solved if we manage to prove
$\displaystyle\frac{3(a+b)^2+4ab}{4ab}\le \frac{2(a^2+b^2)}{ab}.$
This is equivalent to $3a^2+3b^2+10ab\le 8a^2+8b^2,\,$ or $5a^2+5b^2-10ab\ge 0,\;$ which is simply $5(a-b)\ge 0.$
Solution 2
We employ the obvious $\displaystyle\frac{2\sqrt{ab}}{a+b}\le 1\,$ and $\displaystyle\frac{4ab}{(a+b)^2}\le 1\,$ to obtain
$\displaystyle LHS\le 6+\frac{3(a+b)^2}{4ab}.$
Suffice it to prove that $\displaystyle 6+\frac{3(a+b)^2}{4ab}\le 5+2\left(\frac{a}{b}+\frac{b}{a}\right).$
Now note that
$\displaystyle 1+\frac{3(a+b)^2}{4ab}\le\frac{5}{2}+\frac{3}{4}\left(\frac{a}{b}+\frac{b}{a}\right)\le 2\left(\frac{a}{b}+\frac{b}{a}\right),$
Because $\displaystyle\frac{5}{2}\le\frac{5}{4}\left(\frac{a}{b}+\frac{b}{a}\right).$
Solution 3
Using the AM-GM inequality, $\displaystyle\frac{a+b}{2}\ge\sqrt{ab}\,$ and $\displaystyle\frac{2}{a+b}\le\frac{1}{\sqrt{ab}},$
$\displaystyle\begin{align} LHS &\le \left(\sqrt{ab}+\sqrt{ab}+\frac{a+b}{2}\right)\left(\frac{a+b}{2ab}+\frac{1}{\sqrt{ab}}+\frac{1}{\sqrt{ab}}\right)\\ &= \left(2\sqrt{ab}+\frac{a+b}{2}\right)\left(\frac{a+b}{2ab}+\frac{2}{\sqrt{ab}}\right)\\ &=\frac{a+b}{\sqrt{ab}}+4+\frac{(a+b)^2}{4ab}+\frac{a+b}{\sqrt{ab}}\\ &= 4+\frac{(a+b)^2}{4ab}+\frac{2(a+b)}{\sqrt{ab}}. \end{align}$
Thus, suffice it to prove that
$\displaystyle 4+\frac{(a+b)^2}{4ab}+\frac{2(a+b)}{\sqrt{ab}}\le 5 +2 \left(\frac{a}{b}+\frac{b}{a}\right),$
which is equivalent to
$\displaystyle \frac{(a+b)^2}{4ab}+\frac{2(a+b)}{\sqrt{ab}}\le 1 +2\frac{a^2+b^2}{ab}=\frac{2a^2+2b^2+ab}{ab}.$
Now, from $\displaystyle\frac{1}{\sqrt{ab}}\le\frac{a+b}{2ab}\,$ we get $\displaystyle\frac{2(a+b)}{\sqrt{ab}}\le\frac{(a+b)^2}{ab},\,$ implying
$\displaystyle \frac{(a+b)^2}{4ab}+\frac{2(a+b)}{\sqrt{ab}}\le \frac{(a+b)^2}{4ab}+\frac{(a+b)^2}{ab}=\frac{5(a+b)^2}{4ab}.$
Thus, suffice it to prove $\displaystyle\frac{5}{4}\frac{(a+b)^2}{ab}\le\frac{2a^2+2b^2+ab}{ab},\,$ i.e.,
$\displaystyle 5a^2+5b^2+10ab\le 8a^2+8b^2+4ab$
which reduces to $3(a-b)^2\ge 0.$
Solution 4
Let
$\displaystyle\begin{align} A &= \left(\frac{2ab}{a+b}+\sqrt{ab}+\frac{a+b}{2}\right)\left(\frac{a+b}{2ab} + \frac{1}{\sqrt{ab}}+\frac{2}{a+b}\right)\\ &=\left(\frac{2ab}{a+b}+\sqrt{ab}+\frac{a+b}{2}\right)\left(\frac{2}{a+b} + \frac{1}{\sqrt{ab}}+\frac{a+b}{2ab}\right)\\ &=\frac{1}{ab}\left(\frac{2ab}{a+b}+\sqrt{ab}+\frac{a+b}{2}\right)^2\\ &\le\frac{1}{ab}(\sqrt{ab}+a+b)^2\\ &=\frac{1}{ab}(ab+2\sqrt{ab}(a+b)+(a+b)^2)\\ &\le\frac{1}{ab}(ab+2(a+b)^2)\\ &=\frac{1}{ab}(5ab+2(a^2+b^2))\\ &=5+2\left(\frac{a}{b}+\frac{b}{a}\right). \end{align}$
Solution 5
Define $\displaystyle x=\frac{2ab}{a+b},\,$ $\displaystyle y=\sqrt{ab},\,$ $\displaystyle z=\frac{a+b}{2}.\,$ We have $x\le y\le z\,$ and $y^2=xz.
$\displaystyle\begin{align} LHS &= \left(\sum_{cycl}x\right)\left(\sum_{cycl}\frac{1}{x}\right)\\ &=\frac{\left(\displaystyle\sum_{cycl}x\right)(xy+yz+zx)}{xyz}\\ &=\frac{\left(\displaystyle\sum_{cycl}x\right)(xy+yz+y^2)}{xyz}\\ &=\frac{(x+y+z)^2}{xz}\\ &=\frac{(x+y+z)^2}{y^2}. \end{align}$
$\displaystyle\begin{align} RHS &= \frac{2a^2+2b^2+5ab}{ab}\\ &= \frac{2(a+b)^2+ab}{ab}\\ &=1+\frac{8z^2}{y^2}. \end{align}$
The required inequality is equivalent to $\displaystyle\frac{(x+y+z)^2}{y^2}\le 1+\frac{8z^2}{y^2}.\,$ which is $(x+y+z)^2-y^2\le 8z^2,\,$ or, $(x+2y+z)(x+z)\le 8z^2.$
Since $x\le y \le z,\,$ $x+2y+z\le 4z\,$ and $x+z\le 2z,\,$ which shows that, indeed, $(x+2y+z)(x+z)\le 8z^2.$
Solution 6
We know that, for positive $a,b,c,$
$\displaystyle \frac{2ab}{a+b}\le\sqrt{ab}\le\frac{a+b}{2}.$
We'll use Schweitzer's inequality:
$\displaystyle\left(\sum_{k=1}^{n}x_k\right)\left(\sum_{k=1}^{n}\frac{1}{x_k}\right)\le\frac{(m+M)^2n^2}{4mM},$
where $x_1,\ldots,x_n\in [m,M],\;$ $m\gt 0.\;$
with $n=3,\;$ $\displaystyle m=x_1=\frac{2ab}{a+b},\;$ $\displaystyle x_2=\sqrt{ab},\;$ and $x_3=\displaystyle\frac{a+b}{2}=M,\;$ we directly get
$\displaystyle\begin{align} A&=\left(\frac{2ab}{a+b}+\sqrt{ab}+\frac{a+b}{2}\right)\left(\frac{a+b}{2ab} + \frac{1}{\sqrt{ab}}+\frac{2}{a+b}\right)\\ &\le 9\frac{\displaystyle\left(\frac{2ab}{a+b}+\frac{a+b}{2}\right)^2}{4ab}\\ &= \frac{9}{4ab}\left[\left(\frac{2ab}{a+b}\right)^2+2ab+\left(\frac{a+b}{2}\right)^2\right]\\ &\le \frac{9}{4ab}\left[(\sqrt{ab})^2+2ab+\left(\frac{a+b}{2}\right)^2\right]\\ &= \frac{9}{4ab}\left[3ab+\left(\frac{a+b}{2}\right)^2\right]\\ &= \frac{9}{16ab}\left[14ab+(a^2+b^2)\right]\\ &=\frac{63}{8}+\frac{9}{16}\left(\frac{a}{b}+\frac{b}{a}\right). \end{align}$
Now, $\displaystyle 1\le\frac{1}{2}\left(\frac{a}{b}+\frac{b}{a}\right).\,$ It then follows that $\displaystyle\frac{23}{8}\le \frac{23}{16}\left(\frac{a}{b}+\frac{b}{a}\right)$ and, subsequently,
$\displaystyle \frac{63}{8}+\frac{9}{16}\left(\frac{a}{b}+\frac{b}{a}\right)\le\frac{40}{8}+\frac{32}{16}\left(\frac{a}{b}+\frac{b}{a}\right)= 5+2\left(\frac{a}{b}+\frac{b}{a}\right).$
Acknowledgment
The problem above has been kindly posted to the CutTheKnotMath facebook page by Dan Sitaru, along with several solutions. Solutions 1,3,5 are by Soumava Chakraborty; Solution 2 by Kevin Soto Palacios; Solution 4 is by Abdallah El Farissi. Solution 6, making use of Schweitzer's inequality, highlighted by Dan Sitaru elsewhere, yields a somewhat better estimate.
Inequalities in Two Variables
- An Inequality with Just Two Variable $\left(\displaystyle\left(\frac{2ab}{a+b}+\sqrt{\frac{a^2+b^2}{2}}\right)\left(\frac{a+b}{2ab} + \sqrt{\frac{2}{a^2+b^2}}\right) \le \frac{(a+b)^2}{ab}\right)$
- An Inequality with Just Two Variable II $\left(\displaystyle\small{\left(\frac{2ab}{a+b}+\sqrt{ab}+\frac{a+b}{2}\right)\left(\frac{a+b}{2ab} + \frac{1}{\sqrt{ab}}+\frac{2}{a+b}\right) \le 5 +2 \left(\frac{a}{b}+\frac{b}{a}\right)}\right).$
- An Inequality with Just Two Variable III $\left(\displaystyle\frac{a}{b\sqrt{2}}+\frac{b\sqrt{2}}{a}+2\left(\frac{\sqrt{a^2+b^2}}{b}+\frac{b}{a^2+b^2}\right)\ge \frac{9\sqrt{2}}{2}\right)$
- An Inequality with Just Two Variables IV $\left(\displaystyle\frac{a+2}{a^2+a+1}+\frac{b+2}{b^2+b+1}\ge \frac{ab+2}{(ab)^2+ab+1}+1\right)$
- An Inequality with Just Two Variables V $\left(\displaystyle \left(\ln\left(\frac{1}{2a}+\frac{1}{2b}\right)\right)^{a+b}\ge \left(\ln\frac{1}{a}\right)^b\left(\ln\frac{1}{b}\right)^a\right)$
- An Inequality with Just Two Variables VI $\left(|x-y|(x+1)(y+1)\le 2\right)$
- An Inequality with Just Two Variable VII $\left(\displaystyle (x^3+y^3)^3(x^2-xy+y^2)\ge x^2y^2\sqrt{xy}(x^2+y^2)^3\right)$
- An Inequality with Just Two Variable VIII $\left(\displaystyle \frac{a^2}{b+2}+\frac{b^3}{a+2}+(2-a)b^2\le 12\right)$
- The power of substitution III: proving an inequality with two variables $\left(\displaystyle\frac{1}{\sqrt{1+a^2}}+\frac{1}{\sqrt{1+b^2}}\le\frac{2}{\sqrt{1+ab}}\right)$
- Simple Yet Uncommon Inequalities with Absolute Value $\left((|x|-|y|)^2\le |x^2-y^2|,\,|\sqrt{|x|}-\sqrt{|y|}|\le\sqrt{|x-y|}\right)$
- An Inequality with Just Two Variable And an Integer $\small{\left(\displaystyle \Bigr(\frac{a}{b^n}+\frac{b}{a^n}\Bigr)\Bigr(\frac{a^n}{b}+\frac{b^n}{a}\Bigr)\Bigr(\frac{a^n}{b^n}+\frac{b}{a}\Bigr)\Bigr(\frac{b^n}{a^n}+\frac{a}{b}\Bigr)\geq 8\left(\sqrt{\displaystyle\left(\frac{a}{b}\right)^{n-1}}+\sqrt{\displaystyle\left(\frac{b}{a}\right)^{n-1}}\right)\right)}$
- An Inequality with Exponents $\left(\displaystyle b^b\cdot e^{a+\frac{1}{a}}\ge 2e^b\right)$
- Problem 790 from Pentagon: an Inequality in Two Variables $\left(\displaystyle\ln \left|\left(\frac{2+\sin 2b}{2+\sin 2a}\right)\right|\leq \frac{2\sqrt{3}}{3}(b-a)\right)$
- An Inequality with Two Variables from Awesome Math $\left(\displaystyle \frac{6ab-b^2}{8a^2+b^2}\lt\sqrt{\frac{a}{b}}\right)$
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73575453
