An Inequality with Just Two Variables VI
Problem
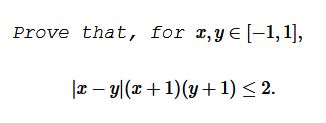
Solution 1
WLOG, $y\ge x.\,$ Let $x=-1+b,\,$ $b\in [0,2].\,$ If $y=x+a=-1+a+b\,$ then $a+b\le 2\,$ because $y\le 1.$
The inequality becomes $ab(a+b)\le 2.\,$ But $ab\le\displaystyle \frac{(a+b)^2}{4},\,$ so that $ab(a+b)\le\displaystyle \frac{(a+b)^3}{4}\le \frac{2^3}{4}=2.\,$
Equality attained for $a=b=1,\,$ i.e., $(x,y)=(0,1)\,$ or $(x,y)=(1,0).$
Solution 2
Set $1+x=a,\,1+y=b.\,$ Then $0\le a,b\le 2,\,$ and we need to show $|a-b|ab\le 2.\,$
WLOG, $a\ge b,\,$ converting inequality into $(a-b)ab\le 2.\,$ By the AM-GM inequality, $\sqrt{(a-b)b}\le\displaystyle \frac{(a-b)+b}{2}=\frac{a}{2},\,$ such that $\displaystyle (a-b)ab\le\frac{a^3}{4}\le\frac{8}{4}=2.\,$ Equality is attained at $a=2\,$ and $a-b=b,\,$ i.e., $b=1.\,$ So the general case of equality is $x=1,\,y=0\,$ or $x=0,\,y=1.$
Solution 3
Since $x,y\in [-1,1],\,$ we can define $x=\cos 2a;\,$ $y=\cos 2b,\,$ where $a,b\in [0,\pi].\,$ We have
$\displaystyle \begin{align} LHS &= \cos 2a-\cos 2b|(\cos 2a+1)(\cos 2b+1)\\ &= 4\cdot|(2\cos^2a-1)-(2\cos^2b-1)|\cos^2a\,\cos^2b\\ &=8\cos^2a\,\cos^2b|\cos^2a-\cos^2b|\\ &\le 8\cos^2a\,\cdot (1-\cos^2a),\,\text{(because}\,|\cos t|\le 1,\,\forall t)\\ &\le 8\frac{\cos^2a+1-\cos^2a}{4}=2. \end{align}$
Equality holds at $2\cos^2=1,\,\cos^2b=1,\,$ i.e., $\cos 2a=0\,$ and $\cos 2b=1,\,$ or $(x,y)=(0,1)\,$ or $(x,y)=(1,0).$
Solution 4
The lower triangle has vertices $(-1,-1),\,$ $(1,-1),\,$ and $(1,1).\,$ Let $p=x+1\,$ and $q=y+1.\,$ Thus, we need to prove $pq(p-q)\le 2\,$ in the triangle with vertices $(0,0),\,$ $(2,0),\,$ and $(2,2)\,$ in the $PQ\,$ plane.
Consider the family of lines $p-q=t,\,$ with $t\in [0,2].\,$ These are parallel lines with varying intercepts and cover the entire triangle. For a fixed value of $t,\,$ the segment of the line in (and on) the triangle is given by $p\in [t,2].$
$\displaystyle \begin{align} LHS &= pq(p-q)=p(p-t)t\\ &=t\left[\left(p-\frac{t}{2}\right)^2-\frac{t^2}{4}\right] \end{align}$
Thus, for a fixed $t,\,$ the maximum value of LHS is
$\displaystyle t\left[\left(2-\frac{t}{2}\right)^2-\frac{t^2}{4}\right]=t(4-2t)=2-2(t-1)^2.$
This is a quadratic function that takes maximum value at $t=1.\,$ The maximum value is $2.$
Illustration
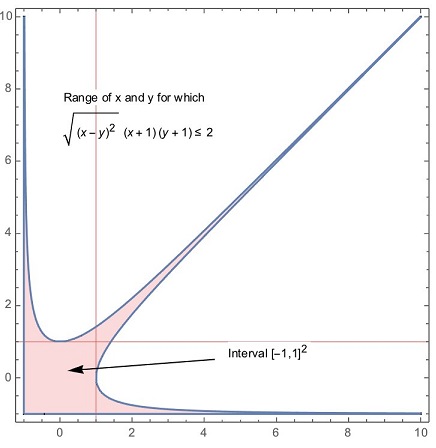
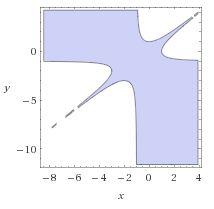
One more
Acknowledgment
The problem has been posted but Nguyen Viet Hung at the mathematical inequalities facebook group and kindly reposted by Leo Giugiuc to the CutTheKnotMath facebook page. Solution 1 is by Imad Zak (Lebanon); Solution 2 is by Leo Giugiuc (Romania); Solution 3 is by Pahm Quy (Vietnam); Solution 4 is by Amit Itagi (USA). The illustration is by N. N. Taleb.
Inequalities in Two Variables
- An Inequality with Just Two Variable $\left(\displaystyle\left(\frac{2ab}{a+b}+\sqrt{\frac{a^2+b^2}{2}}\right)\left(\frac{a+b}{2ab} + \sqrt{\frac{2}{a^2+b^2}}\right) \le \frac{(a+b)^2}{ab}\right)$
- An Inequality with Just Two Variable II $\left(\displaystyle\small{\left(\frac{2ab}{a+b}+\sqrt{ab}+\frac{a+b}{2}\right)\left(\frac{a+b}{2ab} + \frac{1}{\sqrt{ab}}+\frac{2}{a+b}\right) \le 5 +2 \left(\frac{a}{b}+\frac{b}{a}\right)}\right).$
- An Inequality with Just Two Variable III $\left(\displaystyle\frac{a}{b\sqrt{2}}+\frac{b\sqrt{2}}{a}+2\left(\frac{\sqrt{a^2+b^2}}{b}+\frac{b}{a^2+b^2}\right)\ge \frac{9\sqrt{2}}{2}\right)$
- An Inequality with Just Two Variables IV $\left(\displaystyle\frac{a+2}{a^2+a+1}+\frac{b+2}{b^2+b+1}\ge \frac{ab+2}{(ab)^2+ab+1}+1\right)$
- An Inequality with Just Two Variables V $\left(\displaystyle \left(\ln\left(\frac{1}{2a}+\frac{1}{2b}\right)\right)^{a+b}\ge \left(\ln\frac{1}{a}\right)^b\left(\ln\frac{1}{b}\right)^a\right)$
- An Inequality with Just Two Variables VI
- An Inequality with Just Two Variable VII $\left(\displaystyle (x^3+y^3)^3(x^2-xy+y^2)\ge x^2y^2\sqrt{xy}(x^2+y^2)^3\right)$
- An Inequality with Just Two Variable VIII $\left(\displaystyle \frac{a^2}{b+2}+\frac{b^3}{a+2}+(2-a)b^2\le 12\right)$
- The power of substitution III: proving an inequality with two variables $\left(\displaystyle\frac{1}{\sqrt{1+a^2}}+\frac{1}{\sqrt{1+b^2}}\le\frac{2}{\sqrt{1+ab}}\right)$
- Simple Yet Uncommon Inequalities with Absolute Value $\left((|x|-|y|)^2\le |x^2-y^2|,\,|\sqrt{|x|}-\sqrt{|y|}|\le\sqrt{|x-y|}\right)$
- An Inequality with Just Two Variable And an Integer $\small{\left(\displaystyle \Bigr(\frac{a}{b^n}+\frac{b}{a^n}\Bigr)\Bigr(\frac{a^n}{b}+\frac{b^n}{a}\Bigr)\Bigr(\frac{a^n}{b^n}+\frac{b}{a}\Bigr)\Bigr(\frac{b^n}{a^n}+\frac{a}{b}\Bigr)\geq 8\left(\sqrt{\displaystyle\left(\frac{a}{b}\right)^{n-1}}+\sqrt{\displaystyle\left(\frac{b}{a}\right)^{n-1}}\right)\right)}$
- An Inequality with Exponents $\left(\displaystyle b^b\cdot e^{a+\frac{1}{a}}\ge 2e^b\right)$
- Problem 790 from Pentagon: an Inequality in Two Variables $\left(\displaystyle\ln \left|\left(\frac{2+\sin 2b}{2+\sin 2a}\right)\right|\leq \frac{2\sqrt{3}}{3}(b-a)\right)$
- An Inequality with Two Variables from Awesome Math $\left(\displaystyle \frac{6ab-b^2}{8a^2+b^2}\lt\sqrt{\frac{a}{b}}\right)$
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73589614
