An Inequality with Just Two Variable VII
Problem
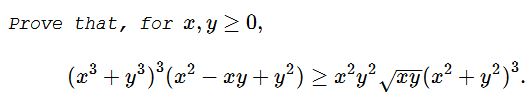
Solution 1
$\displaystyle x^2-xy+y^2\ge\frac{1}{2}(x^2+y^2)\ge\frac{1}{4}(x+y)^2.\,$ Also $x^2+y^2\ge 2xy.$
For $x,y\ge 0,\,$ $x+y\ge 2\sqrt{xy}.$
The given inequality is equivalent to
$\displaystyle (x+y)^3(x^2-xy+y^2)^3(x^2-xy+y^2)\ge x^2y^2\sqrt{xy}(x^2+y^2)^3.$
Thus,
$\displaystyle\begin{align}(x+y)^3(x^2-xy+y^2)&\ge\frac{1}{4}(x+y)^4(x+y)\\ &\ge 8x^2y^2\sqrt{xy},\\ (x^2-xy+y^2)^3&\ge\frac{1}{8}(x^2+y^2)^3 \end{align}$
Multiplying the two gives the require inequality.
Solution 2
$\displaystyle x^3+y^3\ge\frac{1}{2}(x+y)(x^2+y^2).$
By the AM-GM inequality,
$\displaystyle x^2-xy+y^2\ge xy.$
Thus
$\displaystyle (x^3+y^3)^3(x^2-xy+y^2)\ge\frac{xy}{8}(x+y)^2(x^2+y^2)^3\ge RHS$
Because,
$\displaystyle (x+y)^3\ge (2\sqrt{xy})^3=8xy\sqrt{xy}.$
Solution 3
Multiply the require inequality by $(x+y)\,$ which reduce it to:
$\displaystyle (x^3+y^3)^4\ge x^2y^2\sqrt{xy}(x^2+y^2)^3(x+y).$
We have
$\displaystyle \begin{align} (x^3+y^3)^4 &\ge \left(\frac{1}{2}(x+y)(x^2+y^2)\right)^4\\ &=\left(\frac{x+y}{2}\right)^2\cdot \left(\frac{x^2+y^2}{2}\right)\cdot\frac{(x+y)^2}{2}\cdot (x^2+y^2)^3\\ &\ge (xy)^2\cdot \frac{x+y}{2}\cdot (x+y)\cdot (x^2+y^2)^3\\ &\ge (xy)^2\sqrt{xy}(x^2+y^2)^3(x+y). \end{align}$
Solution 4
If $x=0\,$ or $y=0,\,$ there is nothing to prove. Assume $x,y\gt 0.\,$ Set $x=r\cos\theta,\,$ $y=r\sin\theta.\,$ The required inequality reduces to
$r^{11}(\cos^3\theta+\sin^3\theta)^3(\cos^2\theta-\cos\theta\sin\theta+\sin^2\theta)\ge r^{11}(\cos\theta\sin\theta)^{\frac{5}{2}},$
or,
$(\cos\theta+\sin\theta)^3(1-\cos\theta\sin\theta)^4\ge (\cos\theta\sin\theta)^{\frac{5}{2}}.$
By the AM-GM inequality, $\cos\theta+\sin\theta\ge 2\sqrt{\cos\theta\sin\theta}.$ Also, since $2\cos\theta\sin\theta=\sin 2\theta\le 1,\,$ $1-\cos\theta\sin\theta\ge\cos\theta\sin\theta.\,$ In addition,
$\displaystyle \begin{align} 1-\cos\theta\sin\theta &= 1-\frac{1}{2}\left[1-(\cos\theta-\sin\theta)^2\right]\\ &=\frac{1}{2}\left[1+(\cos\theta-\sin\theta)^2\right] \end{align}$
It follows that
$\displaystyle \begin{align} LHS&\ge 8(\cos\theta\sin\theta)^{\frac{3}{2}}(\cos\theta\sin\theta)\times\frac{1}{8}\left[1+(\cos\theta-\sin\theta)^2\right]^3\\ &=(\cos\theta\sin\theta)^{\frac{5}{2}}[\left[1+(\cos\theta-\sin\theta)^2\right]^3\\ &\ge (\cos\theta\sin\theta)^{\frac{5}{2}}=RHS. \end{align}$
Solution 5
From $\displaystyle \sqrt[3]{\frac{x^3+y^3}{2}}\ge\sqrt{\frac{x^2+y^2}{2}},\,$ we have
$2(x^3+y^3)^2\ge (x^2+y^2)^3.$
Also, $x^3+y^3\ge 2\sqrt{x^3y^3}\,$ and $x^2-xy+y^2\ge xy.\,$ Multiplying all three gives the required inequality.
Solution 6
The require inequality is equivalent to
$(x^3+x^3)^4\ge (xy)^{\frac{5}{2}}(x^2+y^2)^3(x+y).$
Now,
$\displaystyle \begin{align} 2(x^3+y^3)^2&\ge (x^2+y^2)^3\\ x^3+y^3&\ge 2(xy)^{\frac{3}{2}}\\ x^3+y^3&\ge \frac{1}{2}(x^2+y^2)(x+y)\\ &\ge\frac{1}{2}\cdot 2\sqrt{x^2y^2}(x+y)\\ &=xy(x+y). \end{align}$
The product of the three yields the required inequality.
Acknowledgment
This problem from his book "Algebraic Phenomenon" has been kindly posted at the CutTheKnotMath facebook page by Dan Sitaru. Solution 1 is by Kevin Soto Palacios; Solution 2 is by Seyran Ibrahimov; Solution 3 by Myagmarsuren Yadamsuren; Solution 4 by Ravi Prakash.
Inequalities in Two Variables
- An Inequality with Just Two Variable $\left(\displaystyle\left(\frac{2ab}{a+b}+\sqrt{\frac{a^2+b^2}{2}}\right)\left(\frac{a+b}{2ab} + \sqrt{\frac{2}{a^2+b^2}}\right) \le \frac{(a+b)^2}{ab}\right)$
- An Inequality with Just Two Variable II $\left(\displaystyle\small{\left(\frac{2ab}{a+b}+\sqrt{ab}+\frac{a+b}{2}\right)\left(\frac{a+b}{2ab} + \frac{1}{\sqrt{ab}}+\frac{2}{a+b}\right) \le 5 +2 \left(\frac{a}{b}+\frac{b}{a}\right)}\right).$
- An Inequality with Just Two Variable III $\left(\displaystyle\frac{a}{b\sqrt{2}}+\frac{b\sqrt{2}}{a}+2\left(\frac{\sqrt{a^2+b^2}}{b}+\frac{b}{a^2+b^2}\right)\ge \frac{9\sqrt{2}}{2}\right)$
- An Inequality with Just Two Variables IV $\left(\displaystyle\frac{a+2}{a^2+a+1}+\frac{b+2}{b^2+b+1}\ge \frac{ab+2}{(ab)^2+ab+1}+1\right)$
- An Inequality with Just Two Variables V $\left(\displaystyle \left(\ln\left(\frac{1}{2a}+\frac{1}{2b}\right)\right)^{a+b}\ge \left(\ln\frac{1}{a}\right)^b\left(\ln\frac{1}{b}\right)^a\right)$
- An Inequality with Just Two Variables VI $\left(|x-y|(x+1)(y+1)\le 2\right)$
- An Inequality with Just Two Variable VII
- An Inequality with Just Two Variable VIII $\left(\displaystyle \frac{a^2}{b+2}+\frac{b^3}{a+2}+(2-a)b^2\le 12\right)$
- The power of substitution III: proving an inequality with two variables $\left(\displaystyle\frac{1}{\sqrt{1+a^2}}+\frac{1}{\sqrt{1+b^2}}\le\frac{2}{\sqrt{1+ab}}\right)$
- Simple Yet Uncommon Inequalities with Absolute Value $\left((|x|-|y|)^2\le |x^2-y^2|,\,|\sqrt{|x|}-\sqrt{|y|}|\le\sqrt{|x-y|}\right)$
- An Inequality with Just Two Variable And an Integer $\small{\left(\displaystyle \Bigr(\frac{a}{b^n}+\frac{b}{a^n}\Bigr)\Bigr(\frac{a^n}{b}+\frac{b^n}{a}\Bigr)\Bigr(\frac{a^n}{b^n}+\frac{b}{a}\Bigr)\Bigr(\frac{b^n}{a^n}+\frac{a}{b}\Bigr)\geq 8\left(\sqrt{\displaystyle\left(\frac{a}{b}\right)^{n-1}}+\sqrt{\displaystyle\left(\frac{b}{a}\right)^{n-1}}\right)\right)}$
- An Inequality with Exponents $\left(\displaystyle b^b\cdot e^{a+\frac{1}{a}}\ge 2e^b\right)$
- Problem 790 from Pentagon: an Inequality in Two Variables $\left(\displaystyle\ln \left|\left(\frac{2+\sin 2b}{2+\sin 2a}\right)\right|\leq \frac{2\sqrt{3}}{3}(b-a)\right)$
- An Inequality with Two Variables from Awesome Math $\left(\displaystyle \frac{6ab-b^2}{8a^2+b^2}\lt\sqrt{\frac{a}{b}}\right)$
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73566930
