Simple Yet Uncommon Inequalities with Absolute Value

Problem

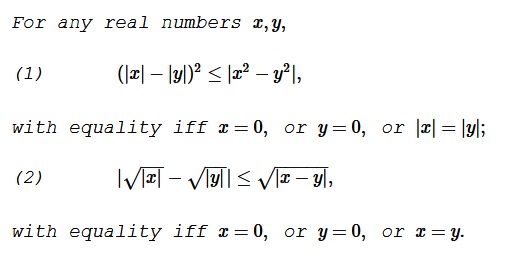
Solution of (1)

For convenience, replace (1) with $(|x|-|y|)^2\le ||x|^2-|y|^2|.\,$ WLOG, assume $|x|\ge |y|.\,$ Then the inequality reduces to

$|x|^2-2\cdot |x|\cdot |y|+|y|^2\le |x|^2-|y|^2,$

or, $2\cdot |y|^2\le 2\cdot |x|\cdot |y|,\,$ which is true by our assumption.

There is clearly equality when $|x|=|y|\,$ or when one of $x,y\,$ equals $0.$

Solution of (2)

Assume first $x\ge y\ge 0.\,$ Then we have to prove that \sqrt{x}-\sqrt{y}\le \sqrt{x-y}.\,$ By squaring we get an inequality reminiscent of (1):

$x+y-2\sqrt{xy}\le x-y,$

or, $2y\le 2\sqrt{xy}\,$ which is true, due to our assumption. Equality is attained when $x=y,\,$ or either $x=0\,$ or $y=0.$

Assume not that $x\ge 0\ge y\,$ and let $z=-y.\,$ After squaring the inequality becomes

$x+z-2\sqrt{xz}\le x+z,$

which is obvious. With equality when $x=0\,$ or $y=0.\,$ Owning to the symmetry of the absolute value $(|-a|=|a|)\,$ there's no need to consider additional cases.

Acknowledgment

This is theorem 11 from D. S. Mitrinović's Analytic Inequalities (This is an expensive book but is also available as a pdf from several sites.)

Inequalities in Two Variables

An Inequality with Just Two Variable $\left(\displaystyle\left(\frac{2ab}{a+b}+\sqrt{\frac{a^2+b^2}{2}}\right)\left(\frac{a+b}{2ab} + \sqrt{\frac{2}{a^2+b^2}}\right) \le \frac{(a+b)^2}{ab}\right)$
An Inequality with Just Two Variable II $\left(\displaystyle\small{\left(\frac{2ab}{a+b}+\sqrt{ab}+\frac{a+b}{2}\right)\left(\frac{a+b}{2ab} + \frac{1}{\sqrt{ab}}+\frac{2}{a+b}\right) \le 5 +2 \left(\frac{a}{b}+\frac{b}{a}\right)}\right).$
An Inequality with Just Two Variable III $\left(\displaystyle\frac{a}{b\sqrt{2}}+\frac{b\sqrt{2}}{a}+2\left(\frac{\sqrt{a^2+b^2}}{b}+\frac{b}{a^2+b^2}\right)\ge \frac{9\sqrt{2}}{2}\right)$
An Inequality with Just Two Variables IV $\left(\displaystyle\frac{a+2}{a^2+a+1}+\frac{b+2}{b^2+b+1}\ge \frac{ab+2}{(ab)^2+ab+1}+1\right)$
An Inequality with Just Two Variables V $\left(\displaystyle \left(\ln\left(\frac{1}{2a}+\frac{1}{2b}\right)\right)^{a+b}\ge \left(\ln\frac{1}{a}\right)^b\left(\ln\frac{1}{b}\right)^a\right)$
An Inequality with Just Two Variables VI $\left(|x-y|(x+1)(y+1)\le 2\right)$
An Inequality with Just Two Variable VII $\left(\displaystyle (x^3+y^3)^3(x^2-xy+y^2)\ge x^2y^2\sqrt{xy}(x^2+y^2)^3\right)$
An Inequality with Just Two Variable VIII $\left(\displaystyle \frac{a^2}{b+2}+\frac{b^3}{a+2}+(2-a)b^2\le 12\right)$
The power of substitution III: proving an inequality with two variables $\left(\displaystyle\frac{1}{\sqrt{1+a^2}}+\frac{1}{\sqrt{1+b^2}}\le\frac{2}{\sqrt{1+ab}}\right)$
Simple Yet Uncommon Inequalities with Absolute Value
An Inequality with Just Two Variable And an Integer $\small{\left(\displaystyle \Bigr(\frac{a}{b^n}+\frac{b}{a^n}\Bigr)\Bigr(\frac{a^n}{b}+\frac{b^n}{a}\Bigr)\Bigr(\frac{a^n}{b^n}+\frac{b}{a}\Bigr)\Bigr(\frac{b^n}{a^n}+\frac{a}{b}\Bigr)\geq 8\left(\sqrt{\displaystyle\left(\frac{a}{b}\right)^{n-1}}+\sqrt{\displaystyle\left(\frac{b}{a}\right)^{n-1}}\right)\right)}$
An Inequality with Exponents $\left(\displaystyle b^b\cdot e^{a+\frac{1}{a}}\ge 2e^b\right)$
Problem 790 from Pentagon: an Inequality in Two Variables $\left(\displaystyle\ln \left|\left(\frac{2+\sin 2b}{2+\sin 2a}\right)\right|\leq \frac{2\sqrt{3}}{3}(b-a)\right)$
An Inequality with Two Variables from Awesome Math $\left(\displaystyle \frac{6ab-b^2}{8a^2+b^2}\lt\sqrt{\frac{a}{b}}\right)$

71930339