An Inequality with Just Two Variables V
Problem
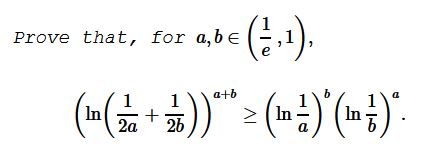
Solution 1
Define function $\displaystyle f:\,\left(\frac{1}{x},1\right)\,\to\,\mathbb{R}\,$ by $\displaystyle \ln\left(\ln\frac{1}{x}\right).\,$ Then
$\displaystyle \begin{align} f'(x)&=\frac{1}{x\ln x}\\ f''(x)&=-\frac{\ln x+1}{(x\ln x)^2}\lt 0,\,\forall x\in\left(\frac{1}{e},1\right). \end{align}$
Hence, $f\,$ is concave on $\displaystyle \left(\frac{1}{e},1\right).\,$ By Jensen's inequality,
$\displaystyle f\left(\frac{b}{a+b}\cdot a+\frac{a}{a+b}\cdot b\right)\ge\frac{b}{a+b}f(a)+\frac{a}{a+b}f(a),$
i.e., $\displaystyle f\left(\frac{2ab}{a+b}\right)\ge\frac{bf(a)}{a+b}+\frac{af(b)}{a+b}.$ To continue,
$\displaystyle \ln\left(\ln\frac{a+b}{2ab}\right)\ge\frac{b}{a+b}\ln\left(\ln\frac{1}{a}\right)+\frac{a}{a+b}\ln\left(\ln\frac{1}{b}\right),$
i.e.,
$\displaystyle \ln\left(\ln\left(\frac{1}{2a}+\frac{1}{2b}\right)\right)\ge\ln\left(\left(\ln\frac{1}{a}\right)^{\frac{b}{a+b}}\cdot\left(\ln\frac{1}{b}\right)^{\frac{a}{a+b}}\right)$
which is
$\displaystyle \ln\left(\frac{1}{2a}+\frac{1}{2b}\right)\ge\left(\left(\ln\frac{1}{a}\right)^{b}\cdot\left(\ln\frac{1}{b}\right)^{a}\right)^{\frac{1}{a+b}}$
and, finally,
$\displaystyle \left(\ln\left(\frac{1}{2a}+\frac{1}{2b}\right)\right)^{a+b}\ge\left(\ln\frac{1}{a}\right)^{b}\cdot\left(\ln\frac{1}{b}\right)^{a}.$
Solution 2
Let $\displaystyle x=\frac{1}{a}\,$ and $\displaystyle y=\frac{1}{b};\,$ $x,y\in (1,e).\,$ We need to show that
$\displaystyle \ln\frac{x+y}{2}\ge\ln(x)^{\frac{x}{x+y}}\ln(y)^{\frac{y}{x+y}}.$
Let $y=x+\epsilon,\,$ where $0\lt\epsilon\lt e-x.\,$ We need to show that
$\displaystyle \ln\frac{2x+\epsilon}{2}\ge\ln(x)^{\frac{x}{2x+\epsilon}}\ln(x+\epsilon)^{\frac{x+\epsilon}{2x+\epsilon}}.$
Expanding up to orders of $\epsilon^2,\,$ $LHS=\ln +\displaystyle \frac{\epsilon}{2x}-\frac{\epsilon^2}{8x^2};\,$ $RHS=\ln x+\frac{\epsilon}{2x}-\frac{\epsilon^2}{8x^2\ln x}.\,$ So, since $\ln a\lt 1,\,$ we have $LHS \ge RHS.\,$
We can refine further with the higher orders of $O(\epsilon^4),\,$ by taking even orders. This is a more engineering oriented but functional approach.
Solution 3
Consider function $\displaystyle F(x)=x\ln (\ln (x)).\,$
$\displaystyle \begin{align} &F'(x)=\ln (\ln (x))+\frac{1}{\ln (x)},\\ &F''(x)=\frac{1}{x\ln (x)}\left[1-\frac{1}{\ln (x)}\right]. \end{align}$
As, for $x\in (1,e),\,$ $0\lt\ln (x)\lt 1,\,$ $F(x)\,$ is a concave function $(F''(x)\lt 0)\,$ for $x\,$ in this range. If so, for any two points $x,y\in (1,e),\,$
$\displaystyle f\left(\frac{x+y}{2}\right)\ge\frac{f(x)+f(y)}{2}.$
Applying this two $F(x)\,$ gives
$\displaystyle \frac{x+y}{2}\cdot\ln\left[\ln\left(\frac{x+y}{2}\right)\right]\ge\frac{x\ln [\ln (x)]+y\ln [\ln (x)]}{2},$
which, after simplification and exponentiation on both sides, yields the required inequality.
Acknowledgment
The problem above has been kindly posted to the CutTheKnotMath facebook page and several other forums (in particular at the Romanian Mathematics Magazine) by Dan Sitaru. After a length of time that it had not gathered any solution, Dan has communicated his solution by private mail. Solution 2 is by N. N. Taleb; Solution 3 is by Michel Charbonneau.
Inequalities in Two Variables
- An Inequality with Just Two Variable $\left(\displaystyle\left(\frac{2ab}{a+b}+\sqrt{\frac{a^2+b^2}{2}}\right)\left(\frac{a+b}{2ab} + \sqrt{\frac{2}{a^2+b^2}}\right) \le \frac{(a+b)^2}{ab}\right)$
- An Inequality with Just Two Variable II $\left(\displaystyle\small{\left(\frac{2ab}{a+b}+\sqrt{ab}+\frac{a+b}{2}\right)\left(\frac{a+b}{2ab} + \frac{1}{\sqrt{ab}}+\frac{2}{a+b}\right) \le 5 +2 \left(\frac{a}{b}+\frac{b}{a}\right)}\right).$
- An Inequality with Just Two Variable III $\left(\displaystyle\frac{a}{b\sqrt{2}}+\frac{b\sqrt{2}}{a}+2\left(\frac{\sqrt{a^2+b^2}}{b}+\frac{b}{a^2+b^2}\right)\ge \frac{9\sqrt{2}}{2}\right)$
- An Inequality with Just Two Variables IV $\left(\displaystyle\frac{a+2}{a^2+a+1}+\frac{b+2}{b^2+b+1}\ge \frac{ab+2}{(ab)^2+ab+1}+1\right)$
- An Inequality with Just Two Variables V
- An Inequality with Just Two Variables VI $\left(|x-y|(x+1)(y+1)\le 2\right)$
- An Inequality with Just Two Variable VII $\left(\displaystyle (x^3+y^3)^3(x^2-xy+y^2)\ge x^2y^2\sqrt{xy}(x^2+y^2)^3\right)$
- An Inequality with Just Two Variable VIII $\left(\displaystyle \frac{a^2}{b+2}+\frac{b^3}{a+2}+(2-a)b^2\le 12\right)$
- The power of substitution III: proving an inequality with two variables $\left(\displaystyle\frac{1}{\sqrt{1+a^2}}+\frac{1}{\sqrt{1+b^2}}\le\frac{2}{\sqrt{1+ab}}\right)$
- Simple Yet Uncommon Inequalities with Absolute Value $\left((|x|-|y|)^2\le |x^2-y^2|,\,|\sqrt{|x|}-\sqrt{|y|}|\le\sqrt{|x-y|}\right)$
- An Inequality with Just Two Variable And an Integer $\small{\left(\displaystyle \Bigr(\frac{a}{b^n}+\frac{b}{a^n}\Bigr)\Bigr(\frac{a^n}{b}+\frac{b^n}{a}\Bigr)\Bigr(\frac{a^n}{b^n}+\frac{b}{a}\Bigr)\Bigr(\frac{b^n}{a^n}+\frac{a}{b}\Bigr)\geq 8\left(\sqrt{\displaystyle\left(\frac{a}{b}\right)^{n-1}}+\sqrt{\displaystyle\left(\frac{b}{a}\right)^{n-1}}\right)\right)}$
- An Inequality with Exponents $\left(\displaystyle b^b\cdot e^{a+\frac{1}{a}}\ge 2e^b\right)$
- Problem 790 from Pentagon: an Inequality in Two Variables $\left(\displaystyle\ln \left|\left(\frac{2+\sin 2b}{2+\sin 2a}\right)\right|\leq \frac{2\sqrt{3}}{3}(b-a)\right)$
- An Inequality with Two Variables from Awesome Math $\left(\displaystyle \frac{6ab-b^2}{8a^2+b^2}\lt\sqrt{\frac{a}{b}}\right)$
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73559789
