Paper Strip Activities
We already had an example of how to transform a paper strip into the Moebius Strip. Here I want to expand on this kind of activity. In short, I plan to describe several surfaces obtained by gluing together sides of a paper strip in various fashions. Note that unless you do something drastic to the strip, the strip is topologically equivalent to a square which means there exists a continuous mapping from one to another.
Amazing results are also obtained by toying with two pieces of paper simultaneously.
First of all let's sum up the results in a table
| Diagram | Properties | Sidedness | Avi movie file size | |
| Cylinder (plane annulus) | Two boundary curves | Two-sided | ||
| Moebius Strip | One boundary curve | One-sided | 267264 bytes | |
| Torus | Closed surface | Two-sided | 389120 bytes | |
| Klein Bottle | Closed surface | One-sided | 389140 bytes | |
| Projective Plane | Closed surface | One-sided |
A few words of explanation are in order. Given a square, we intend to associate (by gluing, if possible) points of its opposite sides. When arrows on the opposite sides point in the same direction as, for example, is the case of the annulus, we identify (glue together) points without twisting the sides. When arrows point in opposite directions one of the sides must be twisted a half turn (180°) before the points are identified. Such is the case of the Moebius Strip.
The last two surfaces (Klein Bottle and Projective Plane) are not realizable in our 3-dimensional space. This is one reason I decided to use the term "identifying the points" instead of "gluing the sides together". It's impossible to form these surfaces in a 3D space.
In what follows we'll try (with the reference to the above diagrams) to figure out what will happen if we attempt to cut the surfaces along either horizontal or vertical lines (this is the first of the promised references).
Remark
My Sliders game is very helpful in reinforcing the notion of side identification introduced below. Success in this game will definitely depend on one's ability to visualize the three closed surfaces (torus, Klein bottle and Projective plane).
Plane Annulus
Vertical cut
Cutting an annulus along a vertical line reduces it back to a square. The vertical solid line on the rightmost diagram is the seam where two sides of the original square have been glued together.
Horizontal cut
Cutting an annulus along a horizontal line results in two separate cylinders of a smaller height. If we cut along the central line, the cylinders will be congruent. Otherwise, one will be taller, another shorter.
Moebius Strip
Vertical cut
Cutting a Moebius strip along a vertical line reduces it back to a square as was the case with the cylinder.
Horizontal cut
The result of cutting the Moebius strip along a horizontal line very much depends on the position of the line in the square.
If the selected line cuts through the middle of the square, we get a strip twice as narrow and twice as long as the original Moebius strip. To ascertain this note that the points A and A' are identical as are the points B and B'. Actually, because of the way we glued the sides of the square, A and A' are one and the same point.
Therefore, we can imagine moving along the upper part of the strip from A to B (which is the same as B') and then moving from B' to A' (which is the same as A) along the lower part of the square. Along the way the side of the square will have twisted twice to the total of 360°. Thus we got a two-sided surface.
We are not finished yet with the Moebius strip. Unlike the cylinder whose border consists of two curves, the border of a Moebius strip consists of a single curve. ![]() Should be start cutting the strip near enough and parallel to the boundary curve we shall eventually produce a thinner Moebius strip (from the middle of the square) and a doubly twisted two-sided surface as we would cutting along the middle line. It's easy to convince oneself of this by imagining the middle part of the square becoming thinner and thinner until the two dotted lines merge into a single one. Which actually shall reduce the picture to the one where we cut along the middle line.
Should be start cutting the strip near enough and parallel to the boundary curve we shall eventually produce a thinner Moebius strip (from the middle of the square) and a doubly twisted two-sided surface as we would cutting along the middle line. It's easy to convince oneself of this by imagining the middle part of the square becoming thinner and thinner until the two dotted lines merge into a single one. Which actually shall reduce the picture to the one where we cut along the middle line.
Remark
Gluing two strips together and cutting them afterwards is a worthwhile activity that brings new entertaining opportunities.
There is an additional page with an interactive Java illustration.
Torus

With the torus the situation is quite simple. Whether it's cut along horizontal or vertical lines, the result is always the same although at first the claim may seem doubtful. When cut along a small circle, the torus becomes a tube. The same is true for a cut along the big circle.
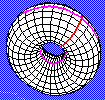
However, this does not seem to jibe with our every day experience. Every one knows that when a bagel is cut along the big circle it splits into two halves. What's wrong with this? A bagel is a solid body whereas the torus, as defined and used here, is a surface. Slicing it into two halves cuts its surface along two circles, not one (Once on the outside of a bagel, then also inside the hole).
Still, vertical and horizontal cuts seem to produce different results. Cutting vertically we get what might be best described as a pipe bent into a circle. Cutting horizontally produces an object that I can easily think of as a flat tire (I would say a very flat tire since it was not just punctured but cut along its biggest circle). That the two surfaces are topologically the same, i.e. one could be continuously transformed into another, follows from the above diagrams. Both can be transformed into an annulus.
Remark
The only cuts I considered on this page are "parallel" to the borders of the generating square. In the case of torus it's also possible to consider slanted cuts. Two cases (the slope is rational or irrational) produce completely different results. I hope to return to the topic of shredding the torus at a later date.
Living on a torus is not the same as living on a plane or even on a sphere. Even games become different. Sam Loyd's 15 requires a different approach when played on a surface of a torus.
Klein Bottle

As I already mentioned, the Klein bottle is not realizable in the usual three-dimensional space. One customary way to visualize it is first to create a tube (cylinder) by gluing together horizontal sides of the square. Next, stretch the tube to make it more amenable to bending and twisting and widen one side of the tube. Lastly, bend the narrow side of the tube towards its wider end. Just before reaching its destination pass the narrow end through the surface of the bottle and glue the two ends from inside the surface. Another way to visualize the bottle is presented in the avi file I refer to in the table above. I do not believe I ever ran into this idea before.

It must be understood that when this operation is carried out in the four dimensional space there is no self-intersections and the two ends of the tube are glued together in the manner of the Moebius strip. What we visualize as the Klein bottle is a projection into our three-dimensional space of a four-dimensional object. It's like projecting a knot onto a plane. You can't help having overlapping pieces of the rope.
Vertical cut
A vertical cut of the Klein bottle reduces it to an annulus. To see this, first swap the two halves of the diagram. Then rotate the (new) right side around its horizontal axis. And, finally, remove the arrows and let the corresponding points overlap.
Horizontal cut

A horizontal cut slices the Klein bottle into two Moebius strips. Start cutting off the central line. As in the case of the Moebius strip, you'll have to run the second part of the cut on another half of the square. Then moving the upper part down and gluing it with the lower part we generate one Moebius strip. Whereas the remaining middle part forms the second one.

Now, what will happen if we start and continue cutting the square along the central line? The avi movie I referred to a couple of times may give you a notion as to the correct answer.
Projective Plane

For the projective plane it does not matter whether one cuts the square vertically or horizontally. Consider a cut that starts on the left of the center line and then continues to the right of it. The right edge of the square is identified (after a twist) with its left edge. So let's position them near each other. Next flip The former right third of the square in the horizontal axis of symmetry and glue to pieces together. Two halves of the upper edge of the resulting figure should be bent towards each other and glued together. The same operation must be applied to the lower edge. What we get is a boat-like surface that one can easily imagine stretched out into a plane disk. The remaining third of the square is a Moebius strip.
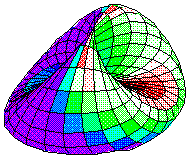
Now, if the original cut goes through the middle of the square all we get is a disk. In order to convert a disk back into the original projective plane endpoints of every diameter should be identified because when we glued two halves together one was flipped in the horizontal axis. Here we learn nothing new. Look at the diagram in the table at the beginning of the page we used to define the projective plane. The fact that the shape in the diagram has corners is topologically irrelevant. What it conveys is that the boundary points symmetrical with respect to the center of the shape (square in the table) must be identified in order to obtain the projective plane.
The reasons for this shape to be called Projective Plane is that it actually models geometry of the plane obtained through a perspecitve transformation.
References
- S. Barr, Experiments in Topology, Dover Publications, 1964
- R. Courant and H. Robbins, What is Mathematics?, Oxford University Press, 1996
- D. Hilbert and S. Cohn-Vossen, Geometry and Imagination, Chelsea Publishing Co, NY 1990.
On Internet
- Moebius Strip
- The Klein Bottle
- The Klein Bottle in Four-Space
- Clifford Pickover's Movie Server
- The Projective Plane
- Figures
|Contact| |Front page| |Contents| |Did you know?| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73581687
