Cardinal Numbers

The key to a definition of cardinal numbers is the notion of a 1-1 correspondence. Two sets are said to be of the same cardinality if there exists a 1-1 correspondence between the two. Two finite sets have the same cardinality only if they have the same number of elements. Their common number of elements serves to denote their cardinality. So the term finite cardinal number is a synonym for natural number. The cardinality of the set {1, 2, 3, 4, 5} is 5. Cardinality of the empty set Ø is 0. A frequent notation for the cardinality of set A is |A|, so that

and

(No less frequent is another one A. I'll be using the vertical bars as more manageable in the HTML environment.)

For finite sets, the cardinality of a proper subset is strictly less than the cardinality of the set itself:

As we know, this is not true for infinite sets. If E is the set of even natural numbers and N the set of all natural numbers then |E| = |N|. The cardinality of both is denoted (pronounced aleph-null or aleph-zero), where 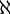is the first letter of the Hebrew alphabet.

The fact that a proper subset of a set may have a cardinality equal to that of the set itself is often taken as the definition of infinite sets: a set is infinite if is contains a proper subset with the same cardinality.

For disjoint finite sets,

The two cases can be combined if we define the addition of two cardinal numbers as the cardinality of the union of two disjoint sets with the given cardinalities. I.e., if we use (2) for any two sets A and B (whether finite or infinite), to define |A| + |B|. In this case, (3) converts to

With all the differences in behavior between finite and infinite sets, it may be surprising that (5) holds for transfinite cardinalities as well. (5) is the content if Cantor-Bernstein-Schroeder theoremSchröder-Bernstein theorem. The theorem comes under many alternative names, e.g. the attributions Cantor-Bernstein-Schroeder theorem, Cantor-Bernstein theorem, Schroeder-Bernstein Theorem, Bernstein's theorem, all usually refer to the same statement.

In order to prove the theorem we need to pay more attention to the "≤" relation as applied to the transfinite cardinals, something we glossed over in (3) and (4).

We say that |A| ≤ |B| if there exists an injection f: A→B. Bernstein's theorem then asserts that if there exists an injection from A to B and another from B to A, then there is a 1-1 correspondence between A and B. (The proof of the theorem appears elsewhere.) We say that |A| < |B| iff |A| ≤ |B| and |A| ≠ |B|.

(6)	S = {aA: af(a)}.

Since f is assumed to be 1-1, it is surjective: there is an sA such that S = f(s). This creates a problem.

Indeed, either s belongs to S or it does not. Let's check the first possibility first. It can't be that sS, because, by definition, S consists of those a for which af(a). So that if sS then, too, sS. We see that it can't be that sS. But sS is also impossible, for if this were the case, s would be an element of S, by the same definition.

It follows that our assumption of the existence of a 1-1 correspondence between A and 2^A leads to a contradiction. The conclusion follows: |A| < |2^A|.

Starting with any set A we may construct a sequence of sets

As a consequence of the theorem, the cardinalities of the sets in sequence (7) are all different. Furthermore,

The set of real numbers, the continuum has the cardinality (also called continuum)

c = .

(This is because the real numbers in the interval [0, 1) when represented in the binary system by the sequences of 0s and 1s can be identified (with some precautions) with subsets of the natural numbers.) Cantor believed but could not prove that

c = ,

i.e., the "next" cardinal number after . The assertion became known as the Continuum Hypothesis (CH): there are no cardinal numbers between and c or, in other words,

(10)

The investigation into CH has been crowned by two results, 25 years apart, that had profound repercussion on the whole notion of the axiomatization of mathematics.

Set Theory, as developed by G. Cantor, is often termed naive as it was based on the intuitive notion of sets and their properties. Everything was a set until it was realized, first by B. Russell, that such an unrestricted handling of sets leads to contradictions. For example, the idea of the "set of all sets" is contradictory. To avoid such constructs and keep Set Theory contradiction-free mathematician came up with several axiomatic systems, of which the one known as Zermelo-Fraenkel (ZF) became the most popular.

In 1939, Kurt Gödel proved that CH does not contradict to ZF and, therefore, could not be disproved based on ZF. In 1963, Paul Cohen proved a similar result for the negation of CH which showed that CH can't be derived from ZF either.

There are many more cardinals than is suggested by (7). There are some with so peculiar construction that they are termed inaccessible (not to the human mind of course). To grasp what are these one needs the notion of a different kind of infinities, viz., the ordinal numbers.

• What Is Infinity?.
• Infinity As a Limit.
  • Infinite Sums and Products
• Cardinal Numbers
  • Cantor-Bernstein-Schroeder theorem.
• Ordinal Numbers.
  • Order. Well-ordered sets.
• Surreal Numbers.
• Infinitesimals. Non-standard Analysis.
• Various Geometric Infinities
  • Projective Infinity.
  • Infinity in Inversive Geometry.
  • Infinity in Compactification.
• Paradoxes of Infinity
  • Achilles and the Tortoise
  • Infinity and Probability
  • Infinite Border, Finite Area