|
|
|
|
|
|
|
|
|
Euclid's Fifth PostulateBesides 23 definitions and several implicit assumptions, Euclid derived much of the planar geometry from five postulates.
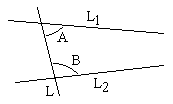
The fifth postulate refers to the diagram on the right. If the sum of two angles A and B formed by a line L and another two lines L1 and L2 sum up to less than two right angles then lines L1 and L2 meet on the side of angles A and B if continued indefinitely. Postulates 1 and 3 set up the "ruler and compass" framework that was a standard for geometric constructions until the middle of the 19th century. They may be said to be based on man's practical experience. The second postulate gives an expression to a commonly held belief that straight lines may not terminate and that the space is unbounded. By the Definition 10, an angle is right if it equals its adjacent angle. Thus the fourth postulate asserts homogeneity of the plane: in whatever directions and through whatever point two perpendicular lines are drawn, the angle they form is one and the same and is called right. We may think of the fourth postulate as having been justified by the everyday experience acquired by man in the finite, inhabited portion of the universe which is our world and extrapolated (much as the Postulate 2) to that part of the world whose existence (and infinite expense) we sense and believe in. Elaborateness of the fifth postulate stands in a stark contrast to the simplicity of the first four. Euclid himself, probably, had mixed feelings about it as he did not make use of it until Proposition I.29. The postulate looks more like another proposition than a basic truth. Here's, for example, Proposition I.27 which, combined with Proposition I.13, claims that, if (in the diagram above) angles A and B sum up to two right angles, then the lines L1 and L2 are parallel.)
(By Definition 23, two straight line in the same plane are parallel if they do not meet even when produced indefinitely in both directions.) Proposition I.17 is actually a converse of the fifth postulate:
The postulate (also known as the Parallel Postulate) attracted immediate attention. The commentator Proclus (c. 410-485) tells us that the postulate was attacked from the very start. He wrote, "This postulate ought even to be struck out of Postulates altogether; for it is a theorem..." Now we know that it is impossible to derive the Parallel Postulate from the first four. The numerous (and failed) attempts to do that gave rise to a slew of statements equivalent to the postulate itself. Several are cited by S.Brodie. Following are a few more:
The last one seems especially intuitive. The reverse holds in non-Euclidean geometries of Lobachevsky and Riemann. Coxeter mentions the fact that Lewis Carroll could not accept this assertion and considered it as a proof of the contradictory nature of non-Euclidean geometries. In one of his books R.Smullyan tells of an experiment he ran in a remedial geometry class. He drew the famous Pythagoras' diagram and asked whether the two small squares are bigger or smaller than the square on the hypotenuse. Half the class thought the sum was bigger, another half thought it was smaller. By all accounts, the Pythagorean Theorem is far from obvious. It is amazing that the Parallel Postulate, being equivalent to such intuitive statements as 1 and 8 above, is also equivalent to the Pythagorean Theorem. 
Copyright © 1996-2008 Alexander Bogomolny |
| 28729413 |  |
|