Graphs Fundamentals
Several puzzles on these pages (Sam Loyd's Fifteen, Sliders, Lucky 7, Happy 8, Blithe 12) could be better understood with the help of the Graph Theory. While it does not immediately offer all the answers it does provide a unified and illuminating approach to these and many other puzzles and games. The Graph Theory originates with a 1736 Leonard Euler's paper "The Seven Bridges of Königsberg". This is how Euler describes the problem:
The problem, which I understand is well known, is stated as follows:
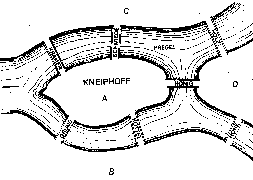
In the town of Königsberg in Prussia (nowadays a city of Kaliningrad in Russia, comment is mine, CTK) there is an island A, called "Kneiphoff", with the two branches of the river (Pregel) flowing around it. There are seven bridges, a, b, c, d, e, f, and g, crossing the two branches.The question is whether a person can plan a walk in such a way that he will cross each of these bridges once but not more than once. I was told that while some deny the possibility of doing this and others were in doubt, there were none who maintained that it was actually possible.On the basis of the above I formulated the following very general problem for myself: Given any configuration of the river and the branches into which it may divide, as well as any number of bridges, to determine whether or not it is possible to cross each bridge exactly once.
I want to sketch a short proof of impossibility to construct such a pass using Graph Theory terms which will be introduced later on. You may skip it and return here later, or you may read through and, perhaps, gain an independent insight into the power of generalization afforded by the Graph Theory.

- The sum of degrees of the vertices of a graph is even
- Every graph has an even number of odd vertices
- If the number of odd vertices is greater than 2 no euler walk exists
- If the number of odd vertices is 2, euler walks exist starting at either of the odd vertices
- With no odd vertices, euler walks can start at an arbitrary vertex
Euler abstracted the bridges into edges and pieces of land into nodes of a graph.
A graph is a collection of nodes (also called vertices) and edges (also called links) each connecting a pair of nodes.
As far as the definitions go, this one is not very good. It's ambiguous for at least two reasons. This definition depends on notions that have not been defined: collection and connecting.
The notion of collection is too fundamental to be treated here. It is indeed customary (under this pretext) to dodge defining a collection by simply appealing to one's common sense (like in, "Collection is a set, aggregation of objects possessing a certain attribute that separates them from all other objects as members of the given set."). I believe everyone agrees that as long as this notion is being used fleetingly as a tool (much like a pencil or a computer) it's OK not to go into details which would definitely divert us from the topic at hand.
But note also that two nodes that define an edge could coalesce into one or can be joined by more than one edge. Thus the "collection" in question is not necessarily a set, but rather a multiset.
The second notion, that of the edges being connections between nodes, is by far too important to the Graph Theory to leave it to one's intuitive perception. It's worse still to conceal the ambiguity of the definition by slipping in a graphic diagram with an immediate appeal to one's intuition. Are the graphs on the two diagrams below the same or not?


Thus, to be more specific, an edge is a 1- or 2-element set with elements drawn from the vertex set. An edge is said to connect the vertices which are its elements. A 1-element edge, i.e. an edge whose ends coincide, is called a loop.
For the visualization sake I shall use the diagrams. I believe it's also OK in so far as they are perceived critically. For example, the two graphs on the diagrams above are of course the same.
Definitions
- Two vertices of a graph are adjacent if they belong to the same edge.
- Elements of an edge are said to be incident to that edge.
- Likewise, an edge is incident to its elements.
- A degree of a vertex is the number of edges incident to it (loops being counted twice).
- A vertex of odd (even) degree is said to be odd (even).
Proposition (the Handshake Lemma)
For a graph, the sum of degrees of all its nodes equals twice the number of edges.
Proof
A degree of a node is the number of edges incident to this node. However every edge is incident to two nodes (or, for a loop, twice to the same node).
Corollary 1
For a graph, the sum of degrees of all its nodes is even.
Corollary 2
In a graph, the number of odd nodes is even.
The applet below is intended to help you with the just introduced concepts. To create a link drag the mouse from one node to another. You may press or release the button either on an existent node or anywhere else. In the latter case, a new node will be created. If the box "Move vertex" is checked you will drag the vertices around instead. The multiplicity of a link is shown by an integer in the middle of the link.
| What if applet does not run? |
The applet may prompt one other observation: the number of odd nodes is always even. Indeed, the sum of all node degrees is even. The sum of the degrees of the even nodes is naturally even. Subtracting one from the other we see that the sum of the degrees of the odd nodes is also even.
M. Gardner quotes a proof by Gerald K. Schoenfeld, a medical officer in the U. S. Navy. Let the nodes denote the participants in a medical convention. The edges represent the handshakes between two participants. Starting at the opening of the convention, as the participants greet each other with shakehands, the edges are being added. At the outset, the number of edges was 0, an even number. A participant is designated odd or even depending on the parity of the number of handshakes he/she took part in up to the given moment. A handshake may occur between three kinds of pairs: odd/odd, even/even, and odd/even. After the handshake, an odd/odd pair becomes even/even, thus the number of odd participants is reduced by 2. An even/even pair becomes odd/odd so that the number of odd participants is increased by 2. The odd/even pair becomes even/odd which does not affect the number of odd participants. We see that a handshake does not change the parity of the number of odd participants. Since at the outset it was even, it will remain even after any number of handshakes.
Definition
- A walk (or a path) of length n on a graph is a sequence v0, e1, v1, e2, ..., vn, where vi are vertices while ei are edges of the graph such that vertices and edges adjacent in the sequence are incident.
- A walk v0, e1, v1, e2, ..., vn is said to connect v0 and vn.
- A walk is closed if
v0n. A closed walk is called a cycle. - A walk which is not closed is open.
- A walk is an euler walk if every edge of the graph appears in the walk exactly once.
- A graph is connected if every two vertices can be connected by a walk.
Proposition
- If a graph has a closed euler walk then every vertex is even.
- If every vertex of a connected graph is even, the graph has an euler walk.
- If a graph has an open euler walk it has exactly two odd vertices.
- If a connected graph has exactly two odd vertices it also has an open euler walk.
Reference
- S. Barr, Experiments in Topology, Dover Publications, 1964
- A. Beck, M. N. Bleicher, D. W. Crowe. Excursions into Mathematics, A K Peters, 2000
- J. L. Casti, Five Golden Rules, John Wiley & Sons, 1996
- S. K. Stein, Mathematics: The Man Made Universe, Dover (January 26, 1999)
- M. Gardner, The Colossal Book of Short Puzzles and Problems, W. W. Norton, 2006, p. 27
- R. J. Trudeau, Introduction to Graph Theory, Dover, NY, 1993.
On Internet
An aside
Königsberg is the birth place of the famous German philosopher Immanuel Kant (1724-1804). I have never visited the place which Kant is known to have never left. Russia annexed this piece of Germany after the World War II. I often wondered if Kant should be considered a great Russian philosopher. After the Baltic states gained their independence from Russia a few years back, the region has no direct link to Russia at all. Below is a part of the map of Kaliningrad, relevant to the discussion:

As you can see, only four bridges remain standing. Had it been this way in Euler's times, the burghers of Königsberg would not be puzzling a problem which attracted Euler's attention. Who knows what event might have triggered the development of Graph Theory and when.
- Graphs Fundamentals
- Crossing Number of a Graph
- Regular Polyhedra
- 3 Utilities Puzzle: Water, Gas, Electricity
- A Clique of Acquaintances
- Round Robin Tournament
- The Affirmative Action Problem
- The Two Men of Tibet Problem
- Euler Cycles in Digraph
- Fleury's Algorithm and Euler's Paths and Cycles: an Interactive Gizmo
- Graph with Nodes of Even Degree
- Graph without 3-Cycles
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73535909
