The Floor Function

Until a few decades ago, [x] was a customary notation for the whole part of a real number x. Nowadays, the floor function notation ⌊x⌋ is at least as widely spread. The latter notation for the floor function and its companion for the ceiling function ⌈x⌉ (which is the least integer not less than x) were introduced by Kenneth Iverson in the early 1960s. Because of the extreme utility and frequency of use, the notations made inroads in mathematics literature. If it were not for the difficulty of typesetting in HTML, I would follow the crowd. As it is, and for the time being, I shall be using the older [x] notation.

For a given real x, [x] denotes the largest integer n that does not exceed x. From the definition, [x] + 1 is always greater than x. [x] = x, for all integer x. For non-integer numbers, [x] is strictly less than x. The inequality [x] ≤ x < [x]+1 always holds. We can now define other functions via formulas that include [x]. Take, for example, f(x) = [sin(x)]. Can you draw the graph of this function?

There are many curiosities related to the floor function. Here are a few spurious examples drawn from an old Russian magazine (Mathematics Education, n1, 1934):

[e]^[π] + [π] = [π]^[e] + [e],

[√2] + [√2] = [√4],

[√3] + [√3] = [√6],

[√8] + [√8] = [√16].

The function has sensible uses as well. Following is a couple of examples where the floor function plays a very meaningful role. In the analysis of Wythoff's game, we had encountered two integer sequences: A and B. The n^th terms in the sequences A and B are expressed as [nφ] and [nφ²], respectively, where φ is the golden ratio (√5 + 1)/2. The Beatty squences generalize this construction.

There is a well known problem whose formulation, perhaps even existence itself, depends on the floor function. In [Ref. 2], it has been designated as a *-problem, to indicate an increased level of difficulty.

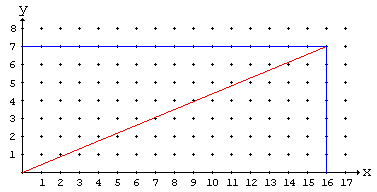
Let, for example, p = 7 and q = 16. Consider a system of Cartesian coordinates. Draw the line connecting the origin with point (q, p). Note that since p and q are assumed to be coprime, the point (q, p) is visible (from the origin.) This is to say that between the origin and the point (q, p), that line contains no other points with integer coordinates. The number of such integer points inside the rectangle formed by points (0, 0), (0, p), (q, 0), and (q, p) is (p - 1)(q - 1). (p - 1)(q - 1)/2 is half that quantity.

The equation of the diagonal line is y = (p/q)x. It only remains to note that for an integer 0 < n, [np/q] is the number of integer points (n, m) below that line. For example, for n = 8, there are [8·7/16] = 3 points, (8, 1), (8, 2), and (8, 3). Since no integer points of the rectangle lie on the diagonal, all such points are either below or above the line. The left-hand side in the required identity counts the number of integer points below the diagonal. As we just saw, the number of such points is (p - 1)(q - 1)/2.

Curiously, from the symmetry (in p and q) of the right side, we also have

[q/p] + [2q/p] + [3q/p] + ... + [(p-1)q/p] = (p-1)(q-1)/2

The graph of the floor function consists of a sequence of unit intervals parallel to the x axis.

The dot at the right end of each segment indicates that the point itself is excluded from the graph. The segments include the left end points but not the right end points. Indeed, [x] is obtained by omitting the fractional part of x, if any. For an integer n and x satisfying n ≤ x < n+1, [x] = n. Therefore, [x] is constant in semi-open intervals [n, n+1). Note the behavior for negative numbers. For example, [-3.5] = -4 in accordance with the definition.

[x] has the property [x + n] = [x] + n. So that integer pieces can be taken in and out of the brackets. The graph of y = [sin(x)] is shown below.

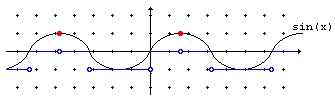
The graph has solitary points (in red) where sine takes value 1 but, otherwise, consists of line segments, some with excluded endpoints (in blue.) The function inherits from sin(x) its period, 2π. You may try to figure out the graph of the function y = sin[x] which is not that nice at all.

To give another application, recollect a remark to the effect that the domain Z[√m] is dense on the real line. The proof can be obtained from two observations. First, for a real x, x - [x] is the fractional part of x, a number between 0 and 1. Apply this to x = √m to obtain a member of Z[√m] that lies in the open interval (0, 1).

Second, for any number a, 0 < a < 1, aⁿ tends to 0 as n grows. Therefore, Z[√m] contains (positive) numbers arbitrarily close to 0. Picking up suitably small numbers with an integer multiple, we may prove that numbers from Z[√m] are dense in the interval [0, 1] and, since Z[√m] contains all the integers, on the whole axis.

1. J. Cofman, What To Solve?, Oxford Science Publications, 1996.
2. D. O. Shklarsky, N. N. Chentzov, I. M. Yaglom, The USSR Olympiad Problem Book, Freeman, 1962

|Contact| |Front page| |Contents| |Algebra| |Store|