What Is Infinity?

One of the most difficult questions a curious student may ask a math teacher is whether 1/0 = ∞ or not. And then of course comes another thoughtful extension: Is 1/∞ = 0?

Why this is a difficult question? It is difficult because it is usually asked by those who feel that infinity is a natural concept, like a number is, and everyone, especially a math teacher, should not have difficulty answering the question. But, for one, it is hard to insist that number is a natural concept. Indeed, while counting numbers have been realized by various cultures, zero and negative numbers were very long in coming, not to mention decimals and complex numbers.

Secondly, even for those numbers that are perceived natural, the concept of division is not fundamental and has to be defined in the course of a study. Addition for natural numbers is an outgrowth of counting and may be easy to define (or accept) for the numbers 1, 2, 3, ... But all the rest (meaning other numbers and operations, like subtraction, multiplication, division) require a definition. So, in the absence of any preliminary understanding or common knowledge, the best (but seldom expected or acceptable) answer is, What do you mean by ∞ or, for that matter, by dividing by 0?

(As an aside, one of the inventors of Calculus - Gottfried Wilhelm Leibniz (1646-1716) - was used to express divergence of the harmonic series thus:

Clearly, at the beginning, intuition played a more important role than rigor. After Leibniz's death, it took about 250 years to set Calculus on a reasonably solid foundation. We are now about 150 year past this landmark, at the time when the standards of mathematical thought and education have evolved dramatically. To be understood by others, it is imperative to fall in line and use the common language.)

Thirdly, even assuming there is a useful definition of infinity that deserves a recognition and a symbol of its own, it is not yet obvious that for this infinity it is possible in a reasonable manner to define arithmetic operations with more common numbers.

Finally, there are many infinities in mathematics; and this is true in more than one sense. There are many infinities and, say, ∞ is not a common notation used to denote each of them. Besides ∞, other symbols, for example, 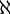and ω, are in circulation that denote infinities very much different from the one (or ones?) that ∞ usually stands for. Various infinities are defined differently and are subject to different operations and different laws. For example, while 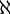+ 1 = 1 + , ω + 1 ≠ 1 + ω.

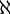It is prudent then to deal with various infinities one at a time. We shall look at several

• What Is Infinity
• Infinity As a Limit.
  • Infinite Sums and Products
• Cardinal Numbers.
  • Cantor-Bernstein-Schroeder theorem.
• Ordinal Numbers.
  • Order. Well-ordered sets.
• Surreal Numbers.
• Infinitesimals. Non-standard Analysis.
• Various Geometric Infinities
  • Projective Infinity.
  • Infinity in Inversive Geometry.
  • Infinity in Compactification.
• Paradoxes of Infinity
  • Achilles and the Tortoise
  • Infinity and Probability
  • Infinite Border, Finite Area

References

1. J. H. Conway, R. K. Guy, The Book of Numbers, Copernicus, 1996
2. W. Dunham, The Calculus Gallery, Princeton University Press, 2008, p. 37
3. K. Kuratowski, A. Mostowski, Set Theory, North-Holland; 2nd revised edition (1976)
4. E. Maor, To Infinity and Beyond, Princeton University Press, 1991
5. R. Rucker, Infinity and the Mind, Princeton University Press, 1995
6. I. Stewart, Concepts of Modern Mathematics, Dover, 1995