Ramsey's Number R(4, 3)

Ramsey's Number R(4, 3) is the least integer N that solves the following problem

In any group of N people either there are 4 that know each other or there are 3 that do not know each other.

Associating the persons in the group with nodes of a graph in which edges join mutual acquaintances the above description could be reformulated as

Any graph with at least R(4, 3) nodes contains either a K₄ or three pairwise disjoined nodes.

A graph is a pair of sets: a set of nodes and a set of edges. Two graphs are said to be complementary if they have the same nodes and disjoined sets of edges whose union consists of all possible edges joing their nodes. Each of the graphs is called a complement of the other. The complement of graph G is denoted G^c.

We have a third formulation for the Ramsey number R(4, 3):

For a graph G with at least R(4, 3) nodes, either G contains K₄ or G^c contains K₃.

Since the relation between complementary graphs is symmetric, R(4, 3) = R(3, 4).

A fourth formulation arises in the study of chromatic graphs. A graph is n-colored if its of its edges is uniquely associated with (colored in) one of n colors. A 2-colored graph is called bichromatic.

Any bichromatic graph G with at least R(4, 3) nodes, G contains either K₄ of one color or K₃ of the other color.

Proposition 1

R(4, 3) ≤ 10.

Proof

Choose one of the present fellows - say, A. The rest are split into two groups: those that know A (group S) and those that don't (group T). There are just two possibilities: either |S| ≥ 6 or |T| ≥ 4. (Otherwise |S∪T| < 9.)

If |S| ≥ 6, then there are 3 members of S that know each other; together with A they form a group of four mutual acquaintances.

If |T| ≥ 4, then either they all know each other (in which case we are done), some two are strangers. In the latter case, together with A these two form a triple of mutual strangers.

A stronger inequality is obtained in a more formal way:

Proposition 2

R(4, 3) ≤ 9.

Proof

Observe that both R(3, 3) = 6 and R(4, 2) = 4 are even so that we are in a position to apply the inequality

R(m, n) ≤ R(m-1, n) + R(m, n-1) - 1,

Which gives R(4, 3) ≤ R(3, 3) + R(4, 2) - 1 = 6 + 4 - 1 = 9.

Theorem

R(4, 3) = 9.

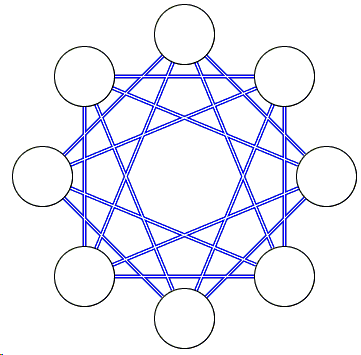
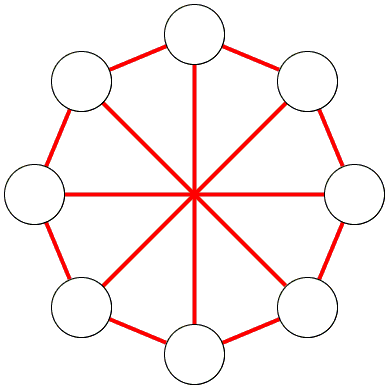
To prove that we need to exhibit a graph with 8 vertices that contains no K₄ and whose complement contains no K₃. Below is one such graph and its complement.

Place 8 nodes on a circle and join all 2- and 3-neighbors. (The immediate neighbor is 1-neighbor, the next is 2-neighbor, and so on.)

Ramsey number R(4, 3)

For the complement, join each node to its immediate neighbors and to the opposite node.

Ramsey number R(4, 3) - complement

References

V. K. Balakrishnan, Theory and Problems of Combinatorics, Schaum's Outline Series, McGraw-Hill, 1995, pp. 22-25

71876526